Selection in spatial stochastic models of cancer: migration as a key modulator of fitness
- PMID: 20406439
- PMCID: PMC2873940
- DOI: 10.1186/1745-6150-5-21
Selection in spatial stochastic models of cancer: migration as a key modulator of fitness
Abstract
Background: We study the selection dynamics in a heterogeneous spatial colony of cells. We use two spatial generalizations of the Moran process, which include cell divisions, death and migration. In the first model, migration is included explicitly as movement to a proximal location. In the second, migration is implicit, through the varied ability of cell types to place their offspring a distance away, in response to another cell's death.
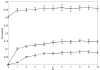
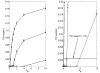
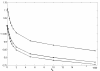
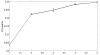
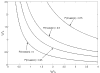
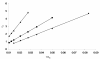
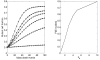
Results: In both models, we find that migration has a direct positive impact on the ability of a single mutant cell to invade a pre-existing colony. Thus, a decrease in the growth potential can be compensated by an increase in cell migration. We further find that the neutral ridges (the set of all types with the invasion probability equal to that of the host cells) remain invariant under the increase of system size (for large system sizes), thus making the invasion probability a universal characteristic of the cells selection status. We find that repeated instances of large scale cell-death, such as might arise during therapeutic intervention or host response, strongly select for the migratory phenotype.
Conclusions: These models can help explain the many examples in the biological literature, where genes involved in cell's migratory and invasive machinery are also associated with increased cellular fitness, even though there is no known direct effect of these genes on the cellular reproduction. The models can also help to explain how chemotherapy may provide a selection mechanism for highly invasive phenotypes.
Figures
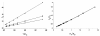
References
-
- Breivik J, Gaudernack G. Carcinogenesis and natural selection: a new perspective to the genetics and epigenetics of colorectal cancer. Adv Cancer Res. 1999;76:187–212. full_text. - PubMed

