Force transduction by the microtubule-bound Dam1 ring

Abstract

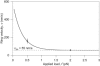
The coupling between the depolymerization of microtubules (MTs) and the motion of the Dam1 ring complex is now thought to play an important role in the generation of forces during mitosis. Our current understanding of this motion is based on a number of detailed computational models. Although these models realize possible mechanisms for force transduction, they can be extended by variation of any of a large number of poorly measured parameters and there is no clear strategy for determining how they might be distinguished experimentally. Here we seek to identify and analyze two distinct mechanisms present in the computational models. In the first, the splayed protofilaments at the end of the depolymerizing MT physically prevent the Dam1 ring from falling off the end, and in the other, an attractive binding secures the ring to the microtubule. Based on this analysis, we discuss how to distinguish between competing models that seek to explain how the Dam1 ring stays on the MT. We propose novel experimental approaches that could resolve these models for the first time, either by changing the diffusion constant of the Dam1 ring (e.g., by tethering a long polymer to it) or by using a time-varying load.

Figure 1

Two general classes of models of Dam1 ring-microtubule coupling. In both cases, the force is Brownian motion; that is, the ring diffuses to the right and the MT happens to unzip one segment or it is driven to the right by a powerstroke associated with unzipping. (Dotted line) Point reached by MT unzipping (x = 0). (A) The ring is sterically confined to the MT by PFs (protofilament model). (B) The ring is attractively bound to the MT surface with a free energy of binding ΔG_Dam1 (binding model). Below each model, the potential profile V in which the ring diffuses is shown as a function of the distance x of the ring from the MT end, and a dotted line indicates the connection between profile and model. The load force is the slope of V(x) for x > 0. In panel A, there is a large (infinite) energy barrier preventing the Dam1 ring moving to x < 0 whenever curled PFs are present. If the PFs completely depolymerize, leaving a blunt end on the MT, this barrier disappears. In panel B, the ring maintains only partial contact as it slides off the end of the MT (–ε < x < 0), which results in a rise in energy until it finally loses contact and is lost forever for x < –ε. See text for details.

Figure 2

Schematic energy landscape underlying PF unzipping. The proposed free energy F landscape of a tubulin dimer at the end of the MT is shown (right) as a function of the distance of the Dam1 ring from the MT end, x, and a reaction coordinate for the unzippering, the angle θ moved by the tubulin dimer (see diagram at left). The diagram is shown for illustrative purposes only and is not quantified in this work. Here θ = 0 represents a dimer in a linear PF incorporated into a stable MT. During unzippering, θ increases and the dimer moves out, ultimately forming the base of a splayed PF. The unzippering is an activated process with an energy barrier (the height of the ridge on the right) that is different for a powerstroke (x < δ) and a burnt-bridges reaction (x > δ), leading to velocities v_ps and v_bb, respectively. The energy landscape must have at least these basic features to give rise to the two depolymerization rates consistent with the data.

Figure 3

The variation of velocity of the Dam1 ring with applied load. The velocity falls as the force increases, because the motion must increasingly rely on the energetic powerstroke. Note that, although the graph appears to suggest an absence of a stalling force, at significantly higher forces the assumption of constant v_ps would fail and the ring would stall. The curve is produced from the best-fit of δ and v_ps in Eq. 4 and data from Franck et al. (12).

Figure 4

Various sketches of a ring on a microtubule. (A) In this configuration the ring is further than δ from the tip of the MT, so the MT depolymerizes with velocity v_bb. Unzipped protofilaments are shown dotted, as they do not affect depolymerization. (B) In some other configuration, the ring is closer to the tip than δ, so the MT depolymerizes with velocity v_ps. (C–F) Detachment mechanisms are shown. This is either insensitive to PFs (C and D, binding model) or sensitive to PFs (E and F, protofilament model). In panels C and E, the ring has not yet escaped. In panels D and F, the ring has escaped from the MT.

Figure 5

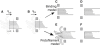
Runtime of the protofilament and binding models. The runtime τ of each model is calculated using the parameters fitted as described in Results and Discussion. Although it may seem that distinguishing the models by varying force is possible due to the differences among their predicted behavior, as shown here, the difference is close to experimental error (±6.15 s) and both models present similar functional form. Only two data points with sufficient statistics were available to perform this fitting (12), making it difficult to draw any conclusions from this approach. The fit provides values for ΔG _Dam1 for the binding model and k_break for the protofilament model.

Figure 6

Model discrimination. The panels show variation of runtime τ with (A) bare MT depolymerization velocity v_bb, (B) diffusion coefficient D, and (C) frequency of applied force ω/2π, for both models under load f = 0.45 pN, chosen because both models predict the same nominal τ and v at this load (see Fig. 5). (A) The runtime τ increases exponentially with v_bb for the protofilament model, whereas the binding model is insensitive. This is because the protofilament model directly depends on v, but the binding model does not. (B) Restricted diffusion suppresses detachment for the binding model because τ is inversely related to D, due to the reduced impetus to escape the potential barrier. The protofilament model, on the other hand, is not affected by D, as t_unzip is independent of D. Distinguishing between models will be easiest by experimental reduction of D, for example by attachment of a long polymer. (C) The binding model is sensitive only to the amplitudes f₀ (here 0.1 pN) and f₁ (here 0.43 pN), not the frequency ω. The rate of detachment for the protofilament model instead strongly depends on the frequency: roughly speaking, the ring is lost more quickly when the high-force part of the cycle persists for long enough for the PFs to completely depolymerize in this time (i.e., when the period is long).