Surprising fitness consequences of GC-biased gene conversion: I. Mutation load and inbreeding depression
- PMID: 20421602
- PMCID: PMC2907210
- DOI: 10.1534/genetics.110.116368
Surprising fitness consequences of GC-biased gene conversion: I. Mutation load and inbreeding depression
Erratum in
- Genetics. 2012 Apr;190(4):1585
Abstract
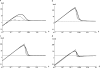
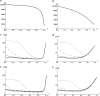
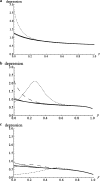
GC-biased gene conversion (gBGC) is a recombination-associated process mimicking selection in favor of G and C alleles. It is increasingly recognized as a widespread force in shaping the genomic nucleotide landscape. In recombination hotspots, gBGC can lead to bursts of fixation of GC nucleotides and to accelerated nucleotide substitution rates. It was recently shown that these episodes of strong gBGC could give spurious signatures of adaptation and/or relaxed selection. There is also evidence that gBGC could drive the fixation of deleterious amino acid mutations in some primate genes. This raises the question of the potential fitness effects of gBGC. While gBGC has been metaphorically termed the "Achilles' heel" of our genome, we do not know whether interference between gBGC and selection merely has practical consequences for the analysis of sequence data or whether it has broader fundamental implications for individuals and populations. I developed a population genetics model to predict the consequences of gBGC on the mutation load and inbreeding depression. I also used estimates available for humans to quantitatively evaluate the fitness impact of gBGC. Surprising features emerged from this model: (i) Contrary to classical mutation load models, gBGC generates a fixation load independent of population size and could contribute to a significant part of the load; (ii) gBGC can maintain recessive deleterious mutations for a long time at intermediate frequency, in a similar way to overdominance, and these mutations generate high inbreeding depression, even if they are slightly deleterious; (iii) since mating systems affect both the selection efficacy and gBGC intensity, gBGC challenges classical predictions concerning the interaction between mating systems and deleterious mutations, and gBGC could constitute an additional cost of outcrossing; and (iv) if mutations are biased toward A and T alleles, very low gBGC levels can reduce the load. A robust prediction is that the gBGC level minimizing the load depends only on the mutational bias and population size. These surprising results suggest that gBGC may have nonnegligible fitness consequences and could play a significant role in the evolution of genetic systems. They also shed light on the evolution of gBGC itself.
Figures


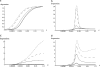



Similar articles
-
Increased Positive Selection in Highly Recombining Genes Does not Necessarily Reflect an Evolutionary Advantage of Recombination.Mol Biol Evol. 2024 Jun 1;41(6):msae107. doi: 10.1093/molbev/msae107. Mol Biol Evol. 2024. PMID: 38829800 Free PMC article.
-
Surprising fitness consequences of GC-biased gene conversion. II. Heterosis.Genetics. 2011 Jan;187(1):217-27. doi: 10.1534/genetics.110.120808. Epub 2010 Oct 18. Genetics. 2011. PMID: 20956611 Free PMC article.
-
A model-based analysis of GC-biased gene conversion in the human and chimpanzee genomes.PLoS Genet. 2013;9(8):e1003684. doi: 10.1371/journal.pgen.1003684. Epub 2013 Aug 15. PLoS Genet. 2013. PMID: 23966869 Free PMC article.
-
Biased gene conversion and the evolution of mammalian genomic landscapes.Annu Rev Genomics Hum Genet. 2009;10:285-311. doi: 10.1146/annurev-genom-082908-150001. Annu Rev Genomics Hum Genet. 2009. PMID: 19630562 Review.
-
Using Computational Simulations to Model Deleterious Variation and Genetic Load in Natural Populations.Am Nat. 2023 Dec;202(6):737-752. doi: 10.1086/726736. Epub 2023 Oct 27. Am Nat. 2023. PMID: 38033186 Free PMC article. Review.
Cited by
-
Factors That Affect the Rates of Adaptive and Nonadaptive Evolution at the Gene Level in Humans and Chimpanzees.Genome Biol Evol. 2022 Feb 4;14(2):evac028. doi: 10.1093/gbe/evac028. Genome Biol Evol. 2022. PMID: 35166775 Free PMC article.
-
Walking through the statistical black boxes of plant breeding.Theor Appl Genet. 2016 Oct;129(10):1933-49. doi: 10.1007/s00122-016-2750-y. Epub 2016 Jul 19. Theor Appl Genet. 2016. PMID: 27435734 Review.
-
GC content of vertebrate exome landscapes reveal areas of accelerated protein evolution.BMC Evol Biol. 2019 Jul 16;19(1):144. doi: 10.1186/s12862-019-1469-1. BMC Evol Biol. 2019. PMID: 31311498 Free PMC article.
-
Compensatory Evolution Following Deleterious Episodes of GC-biased Gene Conversion in Rodents.Mol Biol Evol. 2025 Jul 1;42(7):msaf168. doi: 10.1093/molbev/msaf168. Mol Biol Evol. 2025. PMID: 40629524 Free PMC article.
-
Is Vitamin D Status Associated with Depression, Anxiety and Sleep Quality in Pregnancy: A Systematic Review.Adv Biomed Res. 2020 Jul 27;9:32. doi: 10.4103/abr.abr_188_19. eCollection 2020. Adv Biomed Res. 2020. PMID: 33072644 Free PMC article.
References
-
- Abramowitz, M., and I. A. Stegun, 1970. Handbook of Mathematical Functions. Dover, New York.
-
- Bataillon, T., and M. Kirkpatrick, 2000. Inbreeding depression due to mildly deleterious mutations in finite populations: size does matter. Genet. Res. 75 75–81. - PubMed
-
- Bengtsson, B. O., 1990. The effect of biased conversion on the mutation load. Genet. Res. 55 183–187. - PubMed
-
- Bengtsson, B. O., and M. K. Uyenoyama, 1990. Evolution of the segregation ratio: modification of gene conversion and meiotic drive. Theor. Popul. Biol. 38 192–218. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

