Ion channel density regulates switches between regular and fast spiking in soma but not in axons
- PMID: 20421932
- PMCID: PMC2858683
- DOI: 10.1371/journal.pcbi.1000753
Ion channel density regulates switches between regular and fast spiking in soma but not in axons
Abstract
The threshold firing frequency of a neuron is a characterizing feature of its dynamical behaviour, in turn determining its role in the oscillatory activity of the brain. Two main types of dynamics have been identified in brain neurons. Type 1 dynamics (regular spiking) shows a continuous relationship between frequency and stimulation current (f-I(stim)) and, thus, an arbitrarily low frequency at threshold current; Type 2 (fast spiking) shows a discontinuous f-I(stim) relationship and a minimum threshold frequency. In a previous study of a hippocampal neuron model, we demonstrated that its dynamics could be of both Type 1 and Type 2, depending on ion channel density. In the present study we analyse the effect of varying channel density on threshold firing frequency on two well-studied axon membranes, namely the frog myelinated axon and the squid giant axon. Moreover, we analyse the hippocampal neuron model in more detail. The models are all based on voltage-clamp studies, thus comprising experimentally measurable parameters. The choice of analysing effects of channel density modifications is due to their physiological and pharmacological relevance. We show, using bifurcation analysis, that both axon models display exclusively Type 2 dynamics, independently of ion channel density. Nevertheless, both models have a region in the channel-density plane characterized by an N-shaped steady-state current-voltage relationship (a prerequisite for Type 1 dynamics and associated with this type of dynamics in the hippocampal model). In summary, our results suggest that the hippocampal soma and the two axon membranes represent two distinct kinds of membranes; membranes with a channel-density dependent switching between Type 1 and 2 dynamics, and membranes with a channel-density independent dynamics. The difference between the two membrane types suggests functional differences, compatible with a more flexible role of the soma membrane than that of the axon membrane.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
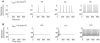
 = 20 µm/s and
= 20 µm/s and  = 5 µm/s. The onset frequency is infinitely small. (B)
= 5 µm/s. The onset frequency is infinitely small. (B)  = 20 µm/s and
= 20 µm/s and  = 5 µm/s. The onset frequency is 30 Hz. Note the damped oscillation with stimulation at 114 mA/m2.
= 5 µm/s. The onset frequency is 30 Hz. Note the damped oscillation with stimulation at 114 mA/m2.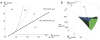
 −
− plane associated with different threshold dynamics. Oscillations occur within the area defined by the continuous line. Double-limit cycle bifurcations in the A2 region, Andronov-Hopf bifurcations (together with double-limit cycle bifurcations) in the B region and saddle-node bifurcations in the C1 region. The bold dashed line indicates the border for channel densities associated with three stationary potentials. The map is a projection of a curved plane in the
plane associated with different threshold dynamics. Oscillations occur within the area defined by the continuous line. Double-limit cycle bifurcations in the A2 region, Andronov-Hopf bifurcations (together with double-limit cycle bifurcations) in the B region and saddle-node bifurcations in the C1 region. The bold dashed line indicates the border for channel densities associated with three stationary potentials. The map is a projection of a curved plane in the  −
− −Istim space (on which the oscillation starts) to the
−Istim space (on which the oscillation starts) to the  −
− plane. (B) The corresponding three-dimensional map, showing the volume associated with oscillations in the
plane. (B) The corresponding three-dimensional map, showing the volume associated with oscillations in the  −
− −Istim space. Oscillations occur in the volume defined by blue and green surfaces. The green surface area represents double-limit cycle bifurcations and the blue area saddle-node bifurcations (SNICs).
−Istim space. Oscillations occur in the volume defined by blue and green surfaces. The green surface area represents double-limit cycle bifurcations and the blue area saddle-node bifurcations (SNICs).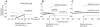
 = 20 µm/s,
= 20 µm/s,  = 2 µm/s. (B) Subcritical Andronov-Hopf and double-limit cycle bifurcations in region B,
= 2 µm/s. (B) Subcritical Andronov-Hopf and double-limit cycle bifurcations in region B,  = 20 µm/s,
= 20 µm/s,  = 10 µm/s. The oscillations emerge at Istim = 84 mA/m2, thus when the corresponding stationary point/voltage still is stable. The loss of stability is due to a double-limit cycle bifurcation, characterized in the variable space by the simultaneous appearance of two limit cycles of opposite stability, one yielding stable and persistent oscillations. This bifurcation is not detectable by the Jacobian matrix of the stationary point; instead the bifurcation depends on the global properties of the variable space. The local Andronov-Hopf bifurcation (also named degenerate Andronov-Hopf bifurcation because of the way the limit cycles collapse onto the equilibrium point [21], [29]) occurs at Istim = 92 mA/m2. There is also an additional Andronov-Hopf bifurcation at higher Istim (524 mA/m2, now shown) that terminates the oscillations. (C) For higher values of
= 10 µm/s. The oscillations emerge at Istim = 84 mA/m2, thus when the corresponding stationary point/voltage still is stable. The loss of stability is due to a double-limit cycle bifurcation, characterized in the variable space by the simultaneous appearance of two limit cycles of opposite stability, one yielding stable and persistent oscillations. This bifurcation is not detectable by the Jacobian matrix of the stationary point; instead the bifurcation depends on the global properties of the variable space. The local Andronov-Hopf bifurcation (also named degenerate Andronov-Hopf bifurcation because of the way the limit cycles collapse onto the equilibrium point [21], [29]) occurs at Istim = 92 mA/m2. There is also an additional Andronov-Hopf bifurcation at higher Istim (524 mA/m2, now shown) that terminates the oscillations. (C) For higher values of  (region A2) these two Andronov-Hopf points collide and disappear (the non-transversal Andronov-Hopf bifurcation), after which no Andronov-Hopf points are present
(region A2) these two Andronov-Hopf points collide and disappear (the non-transversal Andronov-Hopf bifurcation), after which no Andronov-Hopf points are present  = 20 µm/s,
= 20 µm/s,  = 20 µm/s.
= 20 µm/s.
 = 30 µm/s and
= 30 µm/s and  = 5 µm/s. (B)
= 5 µm/s. (B)  = 11 µm/s and
= 11 µm/s and  = 5 µm/s.
= 5 µm/s.
 = 40 µm/s and
= 40 µm/s and  = 15 µm/s. The onset frequency is 8 Hz.
= 15 µm/s. The onset frequency is 8 Hz.
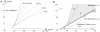
 −
− plane, showing the existence of Type 2 dynamics within region C1. (A) Onset frequencies. (B) Oscillation map for comparison with the map of Fig. 2, showing the subregions C1a and C1b. The border between C1a and C1b closely follows the Bogdanov-Takens bifurcation curve (see Table 1).
plane, showing the existence of Type 2 dynamics within region C1. (A) Onset frequencies. (B) Oscillation map for comparison with the map of Fig. 2, showing the subregions C1a and C1b. The border between C1a and C1b closely follows the Bogdanov-Takens bifurcation curve (see Table 1).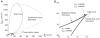
 diagrams at
diagrams at  = 40 µm/s. The thick continuous line defines the region associated with three-root solutions of Equation 17. The thin continuous line is the Andronov-Hopf bifurcation curve and the hatched line, defining the oscillation limit, is the double limit cycle bifurcation curve. (A) An overall perspective. (B) A detailed view of the cusp of the three-root solution space to describe the two subregions, defined by the stability of the stationary potentials. The Bogdanov-Takens bifurcation point is marked.
= 40 µm/s. The thick continuous line defines the region associated with three-root solutions of Equation 17. The thin continuous line is the Andronov-Hopf bifurcation curve and the hatched line, defining the oscillation limit, is the double limit cycle bifurcation curve. (A) An overall perspective. (B) A detailed view of the cusp of the three-root solution space to describe the two subregions, defined by the stability of the stationary potentials. The Bogdanov-Takens bifurcation point is marked.
 = 300 µm/s and
= 300 µm/s and  = 0 µm/s. The onset frequency is 59Hz. (B)
= 0 µm/s. The onset frequency is 59Hz. (B)  = 300 µm/s and
= 300 µm/s and  = 40 µm/s. The onset frequency is 139Hz.
= 40 µm/s. The onset frequency is 139Hz.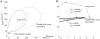
 diagrams at
diagrams at  = 200 µm/s. The thick continuous line defines the region associated with three-root solutions of Equation 14. The thin continuous line is the Andronov-Hopf bifurcation curve and the hatched line is the double limit cycle bifurcation curve. (A) An overall perspective. (B) A detailed view of the cusp of the three-root solution space to describe the subregions.
= 200 µm/s. The thick continuous line defines the region associated with three-root solutions of Equation 14. The thin continuous line is the Andronov-Hopf bifurcation curve and the hatched line is the double limit cycle bifurcation curve. (A) An overall perspective. (B) A detailed view of the cusp of the three-root solution space to describe the subregions.
 = 1200 S/m2 and
= 1200 S/m2 and  = 50 S/m2. Onset frequency is 22 Hz. (B)
= 50 S/m2. Onset frequency is 22 Hz. (B)  = 1200 S/m2 and
= 1200 S/m2 and  = 360 S/m2 (values used by Hodgkin and Huxley in their original study from 1952 [23]). The onset frequency is 52 Hz.
= 360 S/m2 (values used by Hodgkin and Huxley in their original study from 1952 [23]). The onset frequency is 52 Hz.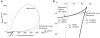
 diagrams at
diagrams at  = 1200 S/m2. The thick continuous line defines the region associated with three-root solutions of Equation 14. The thin continuous line is the Andronov-Hopf bifurcation curve and the hatched line is the double limit cycle bifurcation curve. (A) An overall perspective. (B) A detailed view of the cusp of the three-root solution space to describe the three subregions. The Bogdanov-Takens bifurcation point is marked.
= 1200 S/m2. The thick continuous line defines the region associated with three-root solutions of Equation 14. The thin continuous line is the Andronov-Hopf bifurcation curve and the hatched line is the double limit cycle bifurcation curve. (A) An overall perspective. (B) A detailed view of the cusp of the three-root solution space to describe the three subregions. The Bogdanov-Takens bifurcation point is marked.
 −
− or
or  −
− plane. (A) The frog myelinated axon model. (B) The squid giant axon model. As seen there is no C1a region in any of the maps and consequently both axon models lack Type 1 dynamics. Note also that the myelinated axon model (A) allows oscillations for
plane. (A) The frog myelinated axon model. (B) The squid giant axon model. As seen there is no C1a region in any of the maps and consequently both axon models lack Type 1 dynamics. Note also that the myelinated axon model (A) allows oscillations for  = 0 (no K channels). (C) Onset frequency in the myelinated axon model. (D) Onset frequency in the squid axon model. Circles indicates the original values used by Hodgkin and Huxley for the model of the axon of Loligo forbesi
and Frankenhaeuser and Huxley for model of the sciatic nerve of Xenpus leavis
.
= 0 (no K channels). (C) Onset frequency in the myelinated axon model. (D) Onset frequency in the squid axon model. Circles indicates the original values used by Hodgkin and Huxley for the model of the axon of Loligo forbesi
and Frankenhaeuser and Huxley for model of the sciatic nerve of Xenpus leavis
.References
-
- Tateno T, Robinson HP. Rate coding and spike-time variability in cortical neurons with two types of threshold dynamics. J Neurophysiol. 2006;95:2650–2663. - PubMed
-
- Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Comput. 1996;8:979–1001. - PubMed
-
- Rinzel J, Ermentrout B. Analysis of neural excitability and oscillations. In: Koch C, Segev I, editors. Methods in Neuronal Modeling: From Ions to Networks. Methods in Neuronal Modeling: From Ions to Networks. The MIT Press; 1998. pp. 251–291.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

