Signatures of synchrony in pairwise count correlations

Abstract

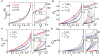
Concerted neural activity can reflect specific features of sensory stimuli or behavioral tasks. Correlation coefficients and count correlations are frequently used to measure correlations between neurons, design synthetic spike trains and build population models. But are correlation coefficients always a reliable measure of input correlations? Here, we consider a stochastic model for the generation of correlated spike sequences which replicate neuronal pairwise correlations in many important aspects. We investigate under which conditions the correlation coefficients reflect the degree of input synchrony and when they can be used to build population models. We find that correlation coefficients can be a poor indicator of input synchrony for some cases of input correlations. In particular, count correlations computed for large time bins can vanish despite the presence of input correlations. These findings suggest that network models or potential coding schemes of neural population activity need to incorporate temporal properties of correlated inputs and take into consideration the regimes of firing rates and correlation strengths to ensure that their building blocks are an unambiguous measures of synchrony.

Keywords: correlation coefficient; count correlations; population models; spike correlations; synchrony.

Figure 1

Generation of spike trains and transformation to spike counts. (A) Generation of spike trains from correlated voltage traces of two neurons with common presynaptic partners. (B) Red and blue vertical bars indicate the spike trains of two neurons. Squares show the boundaries of bins with duration T. n_i(T,t) and n_j(T,t) illustrate corresponding binned spike trains. (C) Firing rate vs. input current in the LIF model (first order solution) and the threshold model (Eq. 11) computed for σ_I = 0.25 (top), I₀ = 0.6 (bottom) and ψ₀ = 1, V_r = 0, τ_M = 15 ms and τ_I = 5 ms.

Figure 2

Dependence of correlation coefficient ρ_ij and conditional rate ν_cond,ij(0) on firing rate and correlation strength. (A, top) ρ_ij vs. ν, (A, bottom) ν_cond,ij(0) vs. ν, as in Eq. 19. (B, top) Pairwise couplings J_ij vs. ν, as in Eq. 5. (B, bottom) c_ij vs. ν. All quantities are computed for τ_s = 10 ms, C(τ) as in Eq. 13 and ν = ν₁ = ν₂; circles denote the corresponding simulation results. ρ_ij, c_ij and J_ij are computed for T = τ_s/4.

Figure 3

Dependence of spike correlation measures on firing rate ν and correlation strength r. (A) ν_cond,ij(0) vs. r (B) ρ_ij vs. r for bin widths T= 30τ_s (red), T= τ_s (blue), T = τ_s/4 (black). (C) c_ij νT vs. r. (D) c_ij vs. r. All quantities are computed for C(τ) as in Eq. 13, correlation time τ_s = 10 ms and three firing rates ν = 2, 4, 6 Hz, ν = ν₁ = ν₂; circles denote simulation results for the corresponding parameters.

Figure 4

Spike correlations and count correlations within a spike train. (A) Example of a binned spike train s_i(t), bins numbered with respect to a reference time bin. (B) ν_cond(τ) vs. τ for τ = 10 ms, numerical solution and simulations for the firing rates ν = 1 Hz (black), 5 Hz (blue) and ν = 10 Hz (red) are superimposed. Dotted lines denote the corresponding solutions for small τ (Eq. 23). (C) Cov(n_i(T,0),n_j(T,τ))/T vs. τ for τ_s = 10 ms, time bin T = τ_s/2 = 5 ms (left), T = 10 ms = τ_s (middle), T = 5τ_s = 50 ms (right). Circles denote the corresponding simulation points, adjacent time bins are denoted by the first points on the time axis. All spike correlations are computed for C(τ) as in Eq. 13.

Figure 5

Influence of temporal structure on pairwise spike correlations. (A) Spike cross correlations ν_cond,ij(τ) and auto correlations ν_cond(τ) for three voltage correlation functions C_i(τ). (B) Voltage correlations $C_1(\text{τ})={\text{σ}}_V^2\text{cosh}{(\text{τ}/{\text{τ}}_s)}^{-1}$ (blue), $C_2(\text{τ})={\text{σ}}_V^2\cosh {(\text{τ}/(\sqrt{2{\text{τ}}_s}))}^{-1}\cos (\text{τ}/\sqrt{2{\text{τ}}_s})$ (red), $C_3(\text{τ})={\text{σ}}_V^2[\exp (-{\text{τ}}^2/(6{\text{τ}}_s^2))-{\text{τ}}^2/(\text{3}{\text{τ}}_s^2)\exp (-{\text{τ}}^2/(6{\text{τ}}_s^2))]$(black). Note, all voltage correlations C_i(τ) share the same correlation time τ_s but have a different functional form. (C) ρ_ij vs. T for voltage correlation functions C_i(τ). For all figures the correlation time τ_s = 10 ms, ν = 5 Hz, ν = ν₁ = ν₂; circles denote the corresponding simulation points.