Atmospheric neutrinos and discovery of neutrino oscillations

Abstract

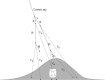
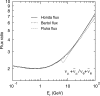
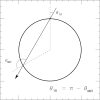
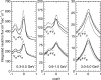
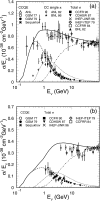
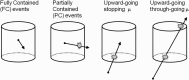
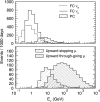
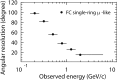
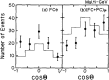
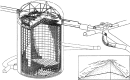
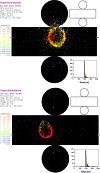
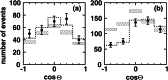
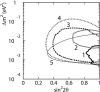
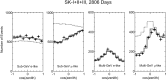
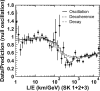
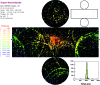
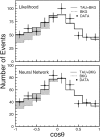
Neutrino oscillation was discovered through studies of neutrinos produced by cosmic-ray interactions in the atmosphere. These neutrinos are called atmospheric neutrinos. They are produced as decay products in hadronic showers resulting from collisions of cosmic rays with nuclei in the atmosphere. Electron-neutrinos and muon-neutrinos are produced mainly by the decay chain of charged pions to muons to electrons. Atmospheric neutrino experiments observed zenith-angle and energy dependent deficit of muon-neutrino events. Neutrino oscillations between muon-neutrinos and tau-neutrinos explain these data well. Neutrino oscillations imply that neutrinos have small but non-zero masses. The small neutrino masses have profound implications to our understanding of elementary particle physics and the Universe. This article discusses the experimental discovery of neutrino oscillations.

Fig. 1

Production of neutrinos by cosmic-ray interactions with the air nucleus in the atmosphere. The typical height of the neutrino production is 15 km above the ground.

Fig. 2

Calculated (ν_μ + ν̄_μ)/(ν_e + ν̄_e) ratio of the atmospheric neutrino flux as a function of the neutrino energy by three independent groups.^–

Fig. 3

A neutrino trajectory that enters the Earth with zenith angle θ_in will exit with a zenith angle θ_out = π − θ_in. As far as the primary fluxes are equal at the entry and exit points, one can deduce the up-down symmetry of the neutrino flux.

Fig. 4

Calculated zenith angle dependence of the atmospheric neutrino flux for several neutrino energy ranges at Kamioka by three independent groups.^– While there is an enhancement of the flux near the horizon, the up-down symmetry is predicted in the energy range above a few GeV.

Fig. 5

Contour map of cut-off rigidity for cosmic rays that produces neutrinos directing to Kamioka. Azimuth angles of 0, 90, 180 and 270 degrees represent directions to south, east, north and west, respectively. The unit is (GeV/c)/Ze, where Ze is the charge of the incident cosmic-ray particle.

Fig. 6

Charged-current total cross sections divided by E_ν for (a) neutrino and (b) anti-neutrino interactions used in the Monte Carlo simulation in the Super-Kamiokande collaboration. Solid line shows the calculated total cross sections. The dashed, dotted and dash-dotted lines show the calculated quasi-elastic, single-meson and deep-inelastic scattering cross sections, respectively. Data points from various experiments are also shown. The references for the original data can also be found in.

Fig. 7

Types of events observed in atmospheric neutrino experiments. Events whose vertex positions are located inside the fiducial volume of the detector and all visible secondary particles stop in the detector are called “fully-contained (FC)” events (left panel). ν_μ events with the multi-GeV neutrino energies produce energetic muons which do not stop in the detector. They are called “partially-contained (PC)” events (second panel from the left). High energy ν_μ interactions in the rock below the detector produce high energy muons. These muons enter into the detector. Some of them stop in the detector (upward stopping muons, second panel from the right) or penetrate through the detector (upward through-going muons, right panel).

Fig. 8

The parent neutrino energy distributions for the fully-contained, partially-contained, upward stopping muon and upward through-going muon events. A cylindrical detector with the fiducial, mass of 22.5 kton is assumed.

Fig. 9

The schematic of the Kamiokande detector. The detector had a cylindrical steel tank which contained 3,000 tons of pure water. Inside this tank, about 1,000 photomultiplier tubes, whose diameter was 50 cm, were used. Later, the outside of the tank was also filled with water of about 1,500 tons, and used as an anti-counter. Thus the total mass of the detector was 4,500 tons.

Fig. 10

Angular correlation between neutrinos and the produced muons for single-Cherenkov-ring events in a water Cherenkov detector (Super-Kamiokande).

Fig. 11

Zenith-angle distributions for multi-GeV (a) e-like and (b) fully-contained plus partially-contained μ-like events observed in Kamiokande, where multi-GeV is defined to be higher than 1.33 GeV in visible energy. Solid histogram shows the predicted distributions without oscillations. Absolute normalization had an uncertainty larger than 20%.

Fig. 12

Schematic of the Super-Kamiokande detector. Each dot seen on the wall shows the 50 cm diameter photomultiplier tube. About 11,200 photomultiplier tubes are used for the inner detector. The outer detector is equipped with about 1,900 20-cm-diameter photomultiplier tubes.

Fig. 13

Candidates of charged-current ν_e (top) and ν_μ (bottom) interactions with visible single Cherenkov ring observed in Super-Kamiokande. The cylindrical detector is opened to flat. The colors indicate the timing of the photon detection and the size of the circles indicates the pulse height for each photomultiplier tube.

Fig. 14

Zenith angle distributions for multi-GeV atmospheric neutrino events reported at the Nuetrino’98 conference based on 535 days exposure of the Super-Kamiokande detector. The left and right panels show the distributions for e-like and μ-like events, respectively. Θ shows the zenith angle, and cos Θ = 1 and −1 represent events whose direction is vertically downward-going and upward-going, respectively.

Fig. 15

Allowed parameter regions of ν_μ → ν_τ oscillations from Super-Kamiokande and Kamiokande shown at the Neutrino’98 conference. Contours are obtained based on; (1) contained events from Super-Kamiokande, (2) contained events from Kamiokande, (3) upward through-going events from Super-Kamiokande, (4) upward through-going events from Kamiokande and (5) stop/through ratio analysis for upward-going muons from Super-Kamiokande.

Fig. 16

Zenith angle distributions observed in SK-I+II+III during 2,806 days of the detector exposure (173 kilo-ton · year). Sub- and multi-GeV fully-contained events are defined to have the visible energy below and above 1.33 GeV, respectively. In the right most panel, PC events are added to the multi-GeV μ-like events. The dotted and solid histograms show the un-oscillated and best-fit oscillated Monte Carlo distributions, respectively.

Fig. 17

Allowed ν_μ → ν_τ neutrino oscillation parameter regions at 68 (dashed lines) and 90% (solid lines) confidence levels (CL) from various experiments. Thick-black and thick-gray lines show the allowed regions based on the zenith-angle analysis and L/E analyses in SK-I+II+III (preliminary), respectively. Also shown are the allowed regions from K2K (thin-gray lines) and MINOS (thin-black lines) long-baseline experiments.

Fig. 18

Data over non-oscillated Monte Carlo for the candidate charged-current ν_μ events are plotted as a function of L/E_ν. The solid histogram shows the Monte Carlo prediction for ν_μ → ν_τ oscillations. The black-dotted and gray-dashed histograms show the Monte Carlo prediction for alternative models that were proposed to explain the zenith angle dependent deficit of the atmospheric neutrino data. Below about L/E_ν less than 100, the data/MC value is about 1 indicating no oscillation effect. Near L/E = 500, there is a clear dip. Above L/E_ν = 500, the data/MC value is about 0.5 corresponding to the averaged ν_μ → ν_μ survival probability. Data from SK-I+II+III are used.

Fig. 19

A simulated charged-current ν_τ interaction in the Super-Kamiokande detector.

Fig. 20

Zenith-angle distributions for the candidate ν_τ events selected from the data observed in SK-I. The upper and lower panels show the results based on the maximum likelihood and neural network methods. Circles with error bars show the data. Solid histograms show the Monte Carlo prediction with ν_μ → ν_τ oscillations but without the charged current ν_τ interactions. The dotted histograms show the fit result with the ν_τ interactions included.