B1 mapping by Bloch-Siegert shift
- PMID: 20432302
- PMCID: PMC2933656
- DOI: 10.1002/mrm.22357
B1 mapping by Bloch-Siegert shift
Abstract
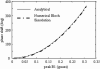
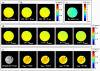
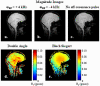
A novel method for amplitude of radiofrequency field (B1+) mapping based on the Bloch-Siegert shift is presented. Unlike conventionally applied double-angle or other signal magnitude-based methods, it encodes the B(1) information into signal phase, resulting in important advantages in terms of acquisition speed, accuracy, and robustness. The Bloch-Siegert frequency shift is caused by irradiating with an off-resonance radiofrequency pulse following conventional spin excitation. When applying the off-resonance radiofrequency in the kilohertz range, spin nutation can be neglected and the primarily observed effect is a spin precession frequency shift. This shift is proportional to the square of the magnitude of B1(2). Adding gradient image encoding following the off-resonance pulse allows one to acquire spatially resolved B(1) maps. The frequency shift from the Bloch-Siegert effect gives a phase shift in the image that is proportional to B(1)(2). The phase difference of two acquisitions, with the radiofrequency pulse applied at two frequencies symmetrically around the water resonance, is used to eliminate undesired off-resonance effects due to amplitude of static field inhomogeneity and chemical shift. In vivo Bloch-Siegert B(1) mapping with 25 sec/slice is demonstrated to be quantitatively comparable to a 21-min double-angle map. As such, this method enables robust, high-resolution B(1)(+) mapping in a clinically acceptable time frame.
(c) 2010 Wiley-Liss, Inc.
Figures



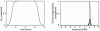



References
-
- Katscher U, Börnert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med. 2003;49:144–150. - PubMed
-
- Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med. 2004;51:775–784. - PubMed
-
- Warntjes JB, Leinhard OD, West J, Lundberg P. Rapid magnetic resonance quantification on the brain: Optimization for clinical usage. Magn Reson Med. 2008;60:320–329. - PubMed
-
- Hornak JP, Szumowski J, Bryant RG. Magnetic field mapping. Magn Reson Med. 1988;6:158–163. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Research Materials

