A critical quantity for noise attenuation in feedback systems
- PMID: 20442870
- PMCID: PMC2861702
- DOI: 10.1371/journal.pcbi.1000764
A critical quantity for noise attenuation in feedback systems
Abstract
Feedback modules, which appear ubiquitously in biological regulations, are often subject to disturbances from the input, leading to fluctuations in the output. Thus, the question becomes how a feedback system can produce a faithful response with a noisy input. We employed multiple time scale analysis, Fluctuation Dissipation Theorem, linear stability, and numerical simulations to investigate a module with one positive feedback loop driven by an external stimulus, and we obtained a critical quantity in noise attenuation, termed as "signed activation time". We then studied the signed activation time for a system of two positive feedback loops, a system of one positive feedback loop and one negative feedback loop, and six other existing biological models consisting of multiple components along with positive and negative feedback loops. An inverse relationship is found between the noise amplification rate and the signed activation time, defined as the difference between the deactivation and activation time scales of the noise-free system, normalized by the frequency of noises presented in the input. Thus, the combination of fast activation and slow deactivation provides the best noise attenuation, and it can be attained in a single positive feedback loop system. An additional positive feedback loop often leads to a marked decrease in activation time, decrease or slight increase of deactivation time and allows larger kinetic rate variations for slow deactivation and fast activation. On the other hand, a negative feedback loop may increase the activation and deactivation times. The negative relationship between the noise amplification rate and the signed activation time also holds for the six other biological models with multiple components and feedback loops. This principle may be applicable to other feedback systems.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
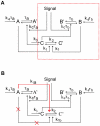
 , loop
, loop  , and output
, and output  .
.  ,
,  , and
, and  denote the active forms, whereas
denote the active forms, whereas  ,
,  , and
, and  stand for the corresponding inactive forms, respectively. The red dashed box represents the single-positive-loop module consisting of
stand for the corresponding inactive forms, respectively. The red dashed box represents the single-positive-loop module consisting of  and
and  only. In the
only. In the  component, signals come in to active
component, signals come in to active  with the help of
with the help of  at the rate of
at the rate of  . All other activation processes of
. All other activation processes of  are lumped into one term, the basal activation rate
are lumped into one term, the basal activation rate  . The conversion from
. The conversion from  to
to  has the rate
has the rate  . In the
. In the  component,
component,  is activated by
is activated by  at the rate of
at the rate of  , and the deactivation of
, and the deactivation of  is at the rate of
is at the rate of  . The basal activation rate of
. The basal activation rate of  is
is  . Similar notations are used in the
. Similar notations are used in the  component. (B) The positive-negative-loop module. The positive feedback from
component. (B) The positive-negative-loop module. The positive feedback from  to
to  is replaced by negative feedback (red arrow).
is replaced by negative feedback (red arrow).
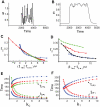
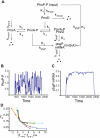
 and
and  (defined in Methods). (B) A typical output response to the signal in (A). (C)
(defined in Methods). (B) A typical output response to the signal in (A). (C)  versus
versus  . Kinetic parameters
. Kinetic parameters  (black),
(black),  (red),
(red),  (green), and
(green), and  (blue) are varied individually to tune
(blue) are varied individually to tune  and
and  while
while  is fixed. The
is fixed. The  curve (black):
curve (black):  ,
,  ; the
; the  curve (red):
curve (red):  ,
,  ; the
; the  curve (green):
curve (green):  ,
,  ; the
; the  curve (blue):
curve (blue):  ,
,  . (D) Four sets of kinetic parameters are chosen, and each set corresponds to one curve. On each curve,
. (D) Four sets of kinetic parameters are chosen, and each set corresponds to one curve. On each curve,  is varied, and the kinetic parameters are fixed. Each point represents an average of
is varied, and the kinetic parameters are fixed. Each point represents an average of  based on
based on  simulations with different noisy signals but fixed
simulations with different noisy signals but fixed  . Set
. Set  (blue):
(blue):  ,
,  ,
,  . Set
. Set  (black):
(black):  ,
,  ,
,  . Set
. Set  (red):
(red):  ,
,  ,
,  . Set
. Set  (green):
(green):  ,
,  ,
,  . In set
. In set  ,
,  takes
takes  ,
,  . For the rest,
. For the rest,  ,
,  . (E)
. (E)  (bottom) and
(bottom) and  (top) versus
(top) versus  . Parameters are the same as the corresponding color set in (D).
. Parameters are the same as the corresponding color set in (D).  ,
,  . (F)
. (F)  (bottom) and
(bottom) and  (top) versus
(top) versus  .
.  (set 1, blue),
(set 1, blue),  (set 2, red). In each plot,
(set 2, red). In each plot,  ,
,  . In all simulations,
. In all simulations,  ,
,  ,
,  , unless otherwise specified.
, unless otherwise specified.
 , where
, where  . (C–D) The change of
. (C–D) The change of  (bottom) and
(bottom) and  (top) with respect to
(top) with respect to  (C) and
(C) and  (D) in single-positive-loop (blue), fast-slow-loop (
(D) in single-positive-loop (blue), fast-slow-loop ( , black), and slow-slow-loop (
, black), and slow-slow-loop ( , red) systems.
, red) systems.  and
and  are varied the same way as in Figure 3E and Figure 3F, respectively. (E–F) The ratio of
are varied the same way as in Figure 3E and Figure 3F, respectively. (E–F) The ratio of  in positive-positive-loop systems to
in positive-positive-loop systems to  in the corresponding single-positive-loop systems with respect to
in the corresponding single-positive-loop systems with respect to  (E) and
(E) and  (F).
(F).  (blue),
(blue),  (black), and
(black), and  (red). All simulations use the same parameters and inputs as their counterparts in Figure 3 with the additional parameter
(red). All simulations use the same parameters and inputs as their counterparts in Figure 3 with the additional parameter  , unless otherwise specified.
, unless otherwise specified.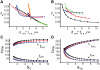
 (black),
(black),  (orange),
(orange),  (red),
(red),  (green),
(green),  (purple),
(purple),  (cyan), and
(cyan), and  (blue) are varied individually to tune
(blue) are varied individually to tune  and
and  while
while  is fixed. In each parameter variation,
is fixed. In each parameter variation,  samples are simulated. (B) The dependence of
samples are simulated. (B) The dependence of  on
on  when
when  is varied and the kinetic parameters are fixed. We use the same four sets of parameters as in Figure 3D with the additional parameters
is varied and the kinetic parameters are fixed. We use the same four sets of parameters as in Figure 3D with the additional parameters  . (C–D) The change of
. (C–D) The change of  (bottom) and
(bottom) and  (top) with respect to
(top) with respect to  (C) and
(C) and  (D) in single-positive-loop (blue), positive-negative-loop (
(D) in single-positive-loop (blue), positive-negative-loop ( , black), and positive-negative-loop (
, black), and positive-negative-loop ( , red) systems.
, red) systems.  and
and  are varied the same way as in Figure 3E and Figure 3F, respectively.
are varied the same way as in Figure 3E and Figure 3F, respectively.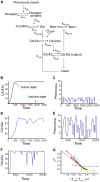
 nM, and the lower red curve is the output response to the low pheromone concentration of [L]
nM, and the lower red curve is the output response to the low pheromone concentration of [L] nM. (C) A noisy input signal with low amplitude. (D) The output response to (C). (E) A noisy input signal with large amplitude. (F) The output response to (E). (G) The noise amplification rate versus the signed activation time. Ten parameters are varied systematically in
nM. (C) A noisy input signal with low amplitude. (D) The output response to (C). (E) A noisy input signal with large amplitude. (F) The output response to (E). (G) The noise amplification rate versus the signed activation time. Ten parameters are varied systematically in  -fold ranges based on their original values given in (D). Each variation corresponds to one curve on the plot. The ten parameters are
-fold ranges based on their original values given in (D). Each variation corresponds to one curve on the plot. The ten parameters are  (red),
(red),  (black),
(black),  (pink),
(pink),  (magenta),
(magenta),  (yellow),
(yellow),  (orange),
(orange),  (cyan),
(cyan),  (green),
(green),  (blue),
(blue),  (brown). The leftmost point of the
(brown). The leftmost point of the  curve is not shown in this picture, as it changes the scale of the picture. Please see Figure S7 for the full plot. Parameter values are mostly taken from , except
curve is not shown in this picture, as it changes the scale of the picture. Please see Figure S7 for the full plot. Parameter values are mostly taken from , except  and
and  , because of the loss of the spatial effect. The initial conditions are
, because of the loss of the spatial effect. The initial conditions are  ,
,  , where
, where  .
.
 -fold ranges based on their original values given in Table S1. The ten parameters are
-fold ranges based on their original values given in Table S1. The ten parameters are  (red),
(red),  (black),
(black),  (pink),
(pink),  (magenta),
(magenta),  (yellow),
(yellow),  (orange),
(orange),  (cyan),
(cyan),  (green),
(green),  (blue),
(blue),  (brown). The equations of the system are given in Section 7 of Text S1.
(brown). The equations of the system are given in Section 7 of Text S1.
 , and
, and  represent the sensor protein in the kinase form, the sensor protein in the phosphatase form, the connector protein, the response regulator, the phosphorylated response regulator, and the connector-sensor(kinase) complex, respectively. (B) The noise amplification rate versus the signed activation time . Eight parameters are varied in
represent the sensor protein in the kinase form, the sensor protein in the phosphatase form, the connector protein, the response regulator, the phosphorylated response regulator, and the connector-sensor(kinase) complex, respectively. (B) The noise amplification rate versus the signed activation time . Eight parameters are varied in  -fold ranges around their original values given in . The eight parameters are
-fold ranges around their original values given in . The eight parameters are  (red),
(red),  (black),
(black),  (pink),
(pink),  (magenta),
(magenta),  (yellow),
(yellow),  (orange),
(orange),  (cyan), and
(cyan), and  (green).
(green).References
-
- Berridge MJ. The versatility and complexity of calcium signalling. Complexity in biological information processing. 2001;239:52–67. - PubMed
-
- Lewis RS. Calcium signaling mechanisms in T lymphocytes. Annu Rev Immunol. 2001;19:497–521. - PubMed
-
- Harris SL, Levine AJ. The p53 pathway: positive and negative feedback loops. Oncogene. 2005;24:2899–2908. - PubMed
-
- Acar M, Becskei A, van Oudenaarden A. Enhancement of cellular memory by reducing stochastic transitions. Nature. 2005;435:228–232. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

