Learning gene regulatory networks from only positive and unlabeled data

Abstract

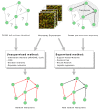
Background: Recently, supervised learning methods have been exploited to reconstruct gene regulatory networks from gene expression data. The reconstruction of a network is modeled as a binary classification problem for each pair of genes. A statistical classifier is trained to recognize the relationships between the activation profiles of gene pairs. This approach has been proven to outperform previous unsupervised methods. However, the supervised approach raises open questions. In particular, although known regulatory connections can safely be assumed to be positive training examples, obtaining negative examples is not straightforward, because definite knowledge is typically not available that a given pair of genes do not interact.

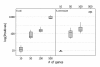
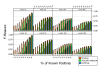
Results: A recent advance in research on data mining is a method capable of learning a classifier from only positive and unlabeled examples, that does not need labeled negative examples. Applied to the reconstruction of gene regulatory networks, we show that this method significantly outperforms the current state of the art of machine learning methods. We assess the new method using both simulated and experimental data, and obtain major performance improvement.

Conclusions: Compared to unsupervised methods for gene network inference, supervised methods are potentially more accurate, but for training they need a complete set of known regulatory connections. A supervised method that can be trained using only positive and unlabeled data, as presented in this paper, is especially beneficial for the task of inferring gene regulatory networks, because only an incomplete set of known regulatory connections is available in public databases such as RegulonDB, TRRD, KEGG, Transfac, and IPA.

Figure 1

Supervised vs unsupervised approaches in the identification of gene-gene interactions. The figure depicts the two main perspectives followed by supervised and unsupervised methods in the inference of gene regulatory networks. Both induce the interaction model from genomic data (e.g. microarray experiments) but supervised methods need also a set of prior known interactions.

Figure 2

Transitive closure heuristic example [20]. The figure shows the PSEUDO-RANDOM negative selection heuristic based on the transitive closure of the known regulatory network.

Figure 3

Distribution of positives in the simulated datasets. The figure shows the distribution of the number of positives in the set of random gene networks generated with the GeneNetWeaver tool.

Figure 4

An example of E. coli 50 gene sub-network generated with the GeneNetWeaver tool. The figure shows a typical gene-gene interaction network generated with the GeneNetWeaver tool. The network is extracted randomly from the complete network of E. coli published in RegulonDB.

Figure 5

Interval plots of F-Measure (95% CI of the mean) of PosOnly, PSEUDO-RANDOM, and SVMOnly classifiers on simulated Escherichia coli and Saccharomyces cerevisiae data. The figure shows the interval plots with 95% confidence interval of PosOnly, PSEUDO-RANDOM, and SVMOnly F-Measure mean obtained on simulated data at different percentage of known positives. All algorithms exhibit a progressively increment in performance when the number of known positive examples grows from P = 10% to P = 100% reaching an almost convergent value at P = 100%.

Figure 6

Average difference between PosOnly, PSEUDO-RANDOM, and SVMOnly classifiers on simulated Escherichia coli and Saccharomyces cerevisiae data. The figure shows the difference between PosOnly, PSEUDO-RANDOM, and SVMOnly F-Measure means at different percentage of known positives and with different network sizes. Such a difference varies with the number of genes and the maximum in the range around P = 40% and P = 60%.

Figure 7

Average Precision of PosOnly, PSEUDO-RANDOM, and SVMOnly classifiers on experimental data. The figure shows the interval plots with 95% confidence interval of PosOnly, PSEUDO-RANDOM, and SVMOnly Precision mean values obtained on experimental data at different percentage of known positives.

Figure 8

Average Recall of PosOnly, PSEUDO-RANDOM, and SVMOnly classifiers on experimental data. The figure shows the interval plots with 95% confidence interval of PosOnly, PSEUDO-RANDOM, and SVMOnly Recall mean values obtained on experimental data at different percentage of known positives.

Figure 9

Average F-Measure of PosOnly, PSEUDO-RANDOM, and SVMOnly classifiers on experimental data. The figure shows the interval plots with 95% confidence interval of PosOnly, PSEUDO-RANDOM, and SVMOnly F-Measure mean obtained on experimental data at different percentage of known positives. Both algorithms exhibit a progressively increment in performance when the number of known positive examples grows from P = 10% to P = 100% reaching an almost convergent value at P = 100%.

Figure 10

Average F-Measure of PosOnly, PSEUDO-RANDOM, and SVMOnly on simulated data and at different network sizes. The figure shows the performance of PosOnly, PSEUDO-RANDOM, and SVMOnly obtained with network of different sizes. Each approaches exhibit similar behavior when the number of genes increases: the average performance of the classifier increases when the percentages of known positives is low, while decreases when the percentages of known positives is high.

Figure 11

Comparison with unsupervised methods, ARACNE and CLR in simulated data. Average F-Measure at different percentage of known positives. The figure shows the difference between supervised and unsupervised methods obtained in the context of simulated data. The performance of supervised methods increases with the percentage of known positive examples. Instead, the performance of unsupervised information theoretic methods decreases with the number of genes in a regulatory network and is of course independent from the percentage of known positive examples. The intersection between supervised and unsupervised curves occur at different percentage of known positives and decreases with the number of genes composing the network.

Figure 12

Comparison with unsupervised methods, ARACNE and CLR in simulated data. Average AUROC at different percentage of known positives. The figure shows the difference between supervised and unsupervised methods performance in terms of AUROC (Area Under the ROC curve) obtained in the context of simulated data. The AUROC of both PosOnly and SVMOnly is the same as the order of data predicted by each method is the same. It can be noticed that, similarly for F-Measure, the performance in term of AUROC of supervised methods increases with the percentage of known positive examples. Instead, the performance of unsupervised information theoretic methods are almost the same explaining the fact that unsupervised methods are able to select very precise top regulations but are unable to uncover (by means of a threshold) the complete set of gene regulations of a network.

Figure 13

Comparison with unsupervised methods, ARACNE and CLR in experimental data. Average F-Measure at different percentage of known positives. The figure shows the difference between supervised and unsupervised methods obtained in the context of experimental data. The performance of supervised methods increases with the percentage of known positive examples. Instead, the performance of unsupervised methods is independent from the percentage of known positive examples.