Robust Tensor Splines for Approximation of Diffusion Tensor MRI Data

Abstract

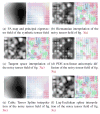
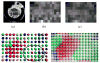
In this paper, we present a novel and robust spline approximation algorithm given a noisy symmetric positive definite (SPD) tensor field. Such tensor fields commonly arise in the field of Medical Imaging in the form of Diffusion Tensor (DT) MRI data sets. We develop a statistically robust algorithm for constructing a tensor product of B-splines - for approximating and interpolating these data - using the Riemannian metric of the manifold of SPD tensors. Our method involves a two step procedure wherein the first step uses Riemannian distances in order to evaluate a tensor spline by computing a weighted intrinsic average of diffusion tensors and the second step involves minimization of the Riemannian distance between the evaluated spline curve and the given data. These two steps are alternated to achieve the desired tensor spline approximation to the given tensor field. We present comparisons of our algorithm with four existing methods of tensor interpolation applied to DT-MRI data from fixed heart slices of a rabbit, and show significantly improved results in the presence of noise and outliers. We also present validation results for our algorithm using synthetically generated noisy tensor field data with outliers. This interpolation work has many applications e.g., in DT-MRI registration, in DT-MRI Atlas construction etc. This research was in part funded by the NIH ROI NS42075 and the Department of Radiology, University of Florida.

Figure 1

Tangent space of the manifold M of diffusion tensors at point p₁. The tangent vector X points to the direction of geodesic γ(t) between the points p₁ and p₂.

Figure 2

A 3rd degree tensor spline S(t), that passes through 5 given tensors p_i of a 1-D tensor field. The given points p_i and the points of the tensor spline S(t) are SPD matrices, elements of the Riemannian manifold M. However the tensor spline is in P(n) × ℜ since the tensors lie on a 1-D lattice. 7 control points c_i are required and 11 knots t_i. The association between basis functions N_i,4(t), knots t_i and given data points p_i are displayed in this figure.

Figure 3

Synthetic tensor fields used in the experiments.

Figure 4

Comparison of interpolation methods.

Figure 5

a)A DT-MRI slice of a rabbit heart. The next figures come from the marked region of this image. b)The Fractional Anisotropy (FA) map of the original data. c)The FA map after the fitting of a cubic tensor spline in the data. d) and e) show the ellipsoid visualization of the corresponding tensor fields.

Figure 6

Real DTI from a rabbit heart: a) FA map of the original data (top), after Log-Euclidean interpolation (middle), after cubic Tensor Spline approximation (bottom). The rest of the plates in this figure depict the dominant eigenvector field of (b) the original data, (c) Log-Euclidean interpolation, (d) Tensor Spline approximation.