Analyzing Neuronal Networks Using Discrete-Time Dynamics
- PMID: 20454529
- PMCID: PMC2864597
- DOI: 10.1016/j.physd.2009.12.011
Analyzing Neuronal Networks Using Discrete-Time Dynamics
Abstract
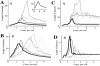
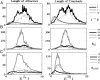
We develop mathematical techniques for analyzing detailed Hodgkin-Huxley like models for excitatory-inhibitory neuronal networks. Our strategy for studying a given network is to first reduce it to a discrete-time dynamical system. The discrete model is considerably easier to analyze, both mathematically and computationally, and parameters in the discrete model correspond directly to parameters in the original system of differential equations. While these networks arise in many important applications, a primary focus of this paper is to better understand mechanisms that underlie temporally dynamic responses in early processing of olfactory sensory information. The models presented here exhibit several properties that have been described for olfactory codes in an insect's Antennal Lobe. These include transient patterns of synchronization and decorrelation of sensory inputs. By reducing the model to a discrete system, we are able to systematically study how properties of the dynamics, including the complex structure of the transients and attractors, depend on factors related to connectivity and the intrinsic and synaptic properties of cells within the network.
Figures



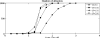




References
-
- Llinas RR. The intrinsic electrophysiological properties of mammalian neurons: Insights into central nervous system function. Science. 1988;242:1654–1664. - PubMed
-
- Jacklet JW. Neuronal and Cellular Oscillators. Marcel Dekker Inc; New York: 1989.
-
- Steriade M, Jones EG, Llinas RR. Thalamic Oscillations and Signaling. Wiley; New York: 1990.
-
- Steriade M, Jones E, McCormick D, editors. Thalamus. II. Elsevier; Amsterdam: 1997.
-
- Traub RD, Miles R. Neuronal Networks of the Hippocampus. Cambridge University Press; New York: 1991.
Grants and funding
LinkOut - more resources
Full Text Sources
