Fractional dynamics pharmacokinetics-pharmacodynamic models
- PMID: 20455076
- PMCID: PMC2889283
- DOI: 10.1007/s10928-010-9159-z
Fractional dynamics pharmacokinetics-pharmacodynamic models
Abstract
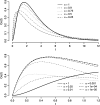
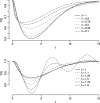
While an increasing number of fractional order integrals and differential equations applications have been reported in the physics, signal processing, engineering and bioengineering literatures, little attention has been paid to this class of models in the pharmacokinetics-pharmacodynamic (PKPD) literature. One of the reasons is computational: while the analytical solution of fractional differential equations is available in special cases, it this turns out that even the simplest PKPD models that can be constructed using fractional calculus do not allow an analytical solution. In this paper, we first introduce new families of PKPD models incorporating fractional order integrals and differential equations, and, second, exemplify and investigate their qualitative behavior. The families represent extensions of frequently used PK link and PD direct and indirect action models, using the tools of fractional calculus. In addition the PD models can be a function of a variable, the active drug, which can smoothly transition from concentration to exposure, to hyper-exposure, according to a fractional integral transformation. To investigate the behavior of the models we propose, we implement numerical algorithms for fractional integration and for the numerical solution of a system of fractional differential equations. For simplicity, in our investigation we concentrate on the pharmacodynamic side of the models, assuming standard (integer order) pharmacokinetics.
Figures




Similar articles
-
CMINNs: Compartment model informed neural networks - Unlocking drug dynamics.Comput Biol Med. 2025 Jan;184:109392. doi: 10.1016/j.compbiomed.2024.109392. Epub 2024 Nov 28. Comput Biol Med. 2025. PMID: 39608036
-
Fractional calculus in bioengineering, part 2.Crit Rev Biomed Eng. 2004;32(2):105-93. doi: 10.1615/critrevbiomedeng.v32.i2.10. Crit Rev Biomed Eng. 2004. PMID: 15373276 Review.
-
Fractional calculus in bioengineering, part 3.Crit Rev Biomed Eng. 2004;32(3-4):195-377. doi: 10.1615/critrevbiomedeng.v32.i34.10. Crit Rev Biomed Eng. 2004. PMID: 15651636 Review.
-
Fractional calculus in bioengineering.Crit Rev Biomed Eng. 2004;32(1):1-104. doi: 10.1615/critrevbiomedeng.v32.i1.10. Crit Rev Biomed Eng. 2004. PMID: 15248549 Review.
-
Fractional calculus in pharmacokinetics.J Pharmacokinet Pharmacodyn. 2018 Feb;45(1):107-125. doi: 10.1007/s10928-017-9547-8. Epub 2017 Oct 3. J Pharmacokinet Pharmacodyn. 2018. PMID: 28975496
Cited by
-
Individualization of a pharmacokinetic model by fractional and nonlinear fit improvement.Eur J Drug Metab Pharmacokinet. 2013 Mar;38(1):69-76. doi: 10.1007/s13318-012-0097-6. Epub 2012 May 23. Eur J Drug Metab Pharmacokinet. 2013. PMID: 22618469
-
Quantitative Systems Pharmacology: A Framework for Context.Curr Pharmacol Rep. 2016 Jun;2(3):152-160. doi: 10.1007/s40495-016-0058-x. Epub 2016 Apr 8. Curr Pharmacol Rep. 2016. PMID: 27570730 Free PMC article.
-
Implementation of non-linear mixed effects models defined by fractional differential equations.J Pharmacokinet Pharmacodyn. 2023 Aug;50(4):283-295. doi: 10.1007/s10928-023-09851-1. Epub 2023 Mar 21. J Pharmacokinet Pharmacodyn. 2023. PMID: 36944853 Free PMC article.
-
The changing face of the rate concept in biopharmaceutical sciences: from classical to fractal and finally to fractional.Pharm Res. 2011 May;28(5):1229-32. doi: 10.1007/s11095-011-0370-4. Epub 2011 Jan 25. Pharm Res. 2011. PMID: 21264680 No abstract available.
-
CMINNs: Compartment model informed neural networks - Unlocking drug dynamics.Comput Biol Med. 2025 Jan;184:109392. doi: 10.1016/j.compbiomed.2024.109392. Epub 2024 Nov 28. Comput Biol Med. 2025. PMID: 39608036
References
-
- Caputo M. Linear models of dissipation whose q is almost frequency independent—II. Geophys J Roy Astron Soc. 1967;13:529–539.
-
- Caputo M, Mainardi F. Linear models of dissipation in anelastic solids. Rivista del Nuovo Cimento. 1971;1:161–198. doi: 10.1007/BF02820620. - DOI
-
- Sokolov IM, Klafter J, Blumen A. Fractional kinetics. Physics Today. 2002;55:48–54. doi: 10.1063/1.1535007. - DOI
-
- Oldham KB, Spanier J. The fractional calculus. San Diego, CA: Academic Press; 1974.
-
- II RJM, Hall MW. Differintegral interpolation from bandlimited signals samples. IEEE Trans Acoust Speech Signal Process. 1981;29:872–877. doi: 10.1109/TASSP.1981.1163636. - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

