Fractional dynamics pharmacokinetics-pharmacodynamic models

Abstract

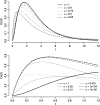
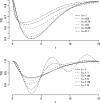
While an increasing number of fractional order integrals and differential equations applications have been reported in the physics, signal processing, engineering and bioengineering literatures, little attention has been paid to this class of models in the pharmacokinetics-pharmacodynamic (PKPD) literature. One of the reasons is computational: while the analytical solution of fractional differential equations is available in special cases, it this turns out that even the simplest PKPD models that can be constructed using fractional calculus do not allow an analytical solution. In this paper, we first introduce new families of PKPD models incorporating fractional order integrals and differential equations, and, second, exemplify and investigate their qualitative behavior. The families represent extensions of frequently used PK link and PD direct and indirect action models, using the tools of fractional calculus. In addition the PD models can be a function of a variable, the active drug, which can smoothly transition from concentration to exposure, to hyper-exposure, according to a fractional integral transformation. To investigate the behavior of the models we propose, we implement numerical algorithms for fractional integration and for the numerical solution of a system of fractional differential equations. For simplicity, in our investigation we concentrate on the pharmacodynamic side of the models, assuming standard (integer order) pharmacokinetics.

Fig. 1

Numerical solutions to the link model equation (12) versus time (t). , Ce (0) = Ce ₀, f(t)=, for different values of α (see text for parameters values). Upper panel (thick solid line): analytic solution for α = 1, thin solid line: indistinguishable from the analytic solution: numerical solution for α = 1; dashed lines: numerical solutions for α = 0.9, 0.75, 0.5, and 0.25, as for the legend in the figure. Lower panel (dashed lines) numerical solutions for α = 0.25, 0.01, 0.001, 0.0001, 0.00001; thick dashed line: f(t) (concentration in the central compartment)

Fig. 2

Numerical solutions to the direct action model equation (16) versus time (t). , Ce(t) computed as in Fig. 1. Upper panel: numerical solutions to for β = 0 (, i.e. drug concentration in the effect compartment), β = 0.1, 0.3, 0.6, 0.9 (i.e. hypo-exposure), β = 1 (, exposure to drug concentration in the effect compartment). Lower panel: for the same values of β

Fig. 3

Numerical solutions to the direct action model equation (16) versus time (t). Upper panel: numerical solutions to , for β = 1, exposure to drug concentration in the effect compartment, for β = 1.25, 1.5, 1.75, hyper-exposure, and for β = 2 quadratic exposure, . Lower panel: for the same values of β

Fig. 4

Numerical solutions to the indirect action model equation (20) versus time (t). , , , Ce(t) computed as in Fig. 1 (see text). Upper panel (solid line): Y(t) corresponding to the standard indirect action model, δ = 1; dashed lines: Y(t) corresponding to the fractional differential equation solved for 0 < δ < 1. Lower panel (solid line): Y(t) for δ = 1; dashed lines: Y(t) for 1 < δ < 2

Fig. 5

Numerical solutions to the indirect action model equation (21) versus time (t). , , , Ce(t) computed as in Fig. 1 (see text). Upper panel (solid line): Y(t) for δ = 1; dashed lines: Y(t) for 0 < δ < 1. Lower panel (solid line): Y(t) for δ = 1; dashed lines: Y(t) for 1 < δ < 2

Fig. 6

Scaled weights of quadrature for the numerical approximation of the Riemann–Liouville fractional integral (Eq. 5) and active drug )