An axisymmetric boundary element model for determination of articular cartilage pericellular matrix properties in situ via inverse analysis of chondron deformation
- PMID: 20459199
- PMCID: PMC3637940
- DOI: 10.1115/1.4000938
An axisymmetric boundary element model for determination of articular cartilage pericellular matrix properties in situ via inverse analysis of chondron deformation
Abstract
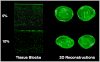
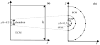
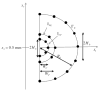
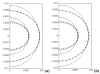
The pericellular matrix (PCM) is the narrow tissue region surrounding all chondrocytes in articular cartilage and, together, the chondrocyte(s) and surrounding PCM have been termed the chondron. Previous theoretical and experimental studies suggest that the structure and properties of the PCM significantly influence the biomechanical environment at the microscopic scale of the chondrocytes within cartilage. In the present study, an axisymmetric boundary element method (BEM) was developed for linear elastic domains with internal interfaces. The new BEM was employed in a multiscale continuum model to determine linear elastic properties of the PCM in situ, via inverse analysis of previously reported experimental data for the three-dimensional morphological changes of chondrons within a cartilage explant in equilibrium unconfined compression (Choi, et al., 2007, "Zonal Changes in the Three-Dimensional Morphology of the Chondron Under Compression: The Relationship Among Cellular, Pericellular, and Extracellular Deformation in Articular Cartilage," J. Biomech., 40, pp. 2596-2603). The microscale geometry of the chondron (cell and PCM) within the cartilage extracellular matrix (ECM) was represented as a three-zone equilibrated biphasic region comprised of an ellipsoidal chondrocyte with encapsulating PCM that was embedded within a spherical ECM subjected to boundary conditions for unconfined compression at its outer boundary. Accuracy of the three-zone BEM model was evaluated and compared with analytical finite element solutions. The model was then integrated with a nonlinear optimization technique (Nelder-Mead) to determine PCM elastic properties within the cartilage explant by solving an inverse problem associated with the in situ experimental data for chondron deformation. Depending on the assumed material properties of the ECM and the choice of cost function in the optimization, estimates of the PCM Young's modulus ranged from approximately 24 kPa to 59 kPa, consistent with previous measurements of PCM properties on extracted chondrons using micropipette aspiration. Taken together with previous experimental and theoretical studies of cell-matrix interactions in cartilage, these findings suggest an important role for the PCM in modulating the mechanical environment of the chondrocyte.
Figures




Similar articles
-
Zonal uniformity in mechanical properties of the chondrocyte pericellular matrix: micropipette aspiration of canine chondrons isolated by cartilage homogenization.Ann Biomed Eng. 2005 Oct;33(10):1312-8. doi: 10.1007/s10439-005-4479-7. Ann Biomed Eng. 2005. PMID: 16240080
-
The dynamic mechanical environment of the chondrocyte: a biphasic finite element model of cell-matrix interactions under cyclic compressive loading.J Biomech Eng. 2008 Dec;130(6):061009. doi: 10.1115/1.2978991. J Biomech Eng. 2008. PMID: 19045538 Free PMC article.
-
The deformation behavior and mechanical properties of chondrocytes in articular cartilage.Osteoarthritis Cartilage. 1999 Jan;7(1):59-70. doi: 10.1053/joca.1998.0162. Osteoarthritis Cartilage. 1999. PMID: 10367015 Review.
-
Alterations in the mechanical properties of the human chondrocyte pericellular matrix with osteoarthritis.J Biomech Eng. 2003 Jun;125(3):323-33. doi: 10.1115/1.1579047. J Biomech Eng. 2003. PMID: 12929236
-
The pericellular matrix as a transducer of biomechanical and biochemical signals in articular cartilage.Ann N Y Acad Sci. 2006 Apr;1068:498-512. doi: 10.1196/annals.1346.011. Ann N Y Acad Sci. 2006. PMID: 16831947 Review.
Cited by
-
The structure and function of the pericellular matrix of articular cartilage.Matrix Biol. 2014 Oct;39:25-32. doi: 10.1016/j.matbio.2014.08.009. Epub 2014 Aug 27. Matrix Biol. 2014. PMID: 25172825 Free PMC article. Review.
-
Theoretically proposed optimal frequency for ultrasound induced cartilage restoration.Theor Biol Med Model. 2017 Nov 14;14(1):21. doi: 10.1186/s12976-017-0067-4. Theor Biol Med Model. 2017. PMID: 29132387 Free PMC article.
-
Biomechanics of meniscus cells: regional variation and comparison to articular chondrocytes and ligament cells.Biomech Model Mechanobiol. 2012 Sep;11(7):1047-56. doi: 10.1007/s10237-012-0372-0. Epub 2012 Jan 10. Biomech Model Mechanobiol. 2012. PMID: 22231673 Free PMC article.
-
A biomechanical role for perlecan in the pericellular matrix of articular cartilage.Matrix Biol. 2012 Jul;31(6):320-7. doi: 10.1016/j.matbio.2012.05.002. Epub 2012 May 30. Matrix Biol. 2012. PMID: 22659389 Free PMC article.
-
Micromechanical mapping of early osteoarthritic changes in the pericellular matrix of human articular cartilage.Osteoarthritis Cartilage. 2013 Dec;21(12):1895-903. doi: 10.1016/j.joca.2013.08.026. Epub 2013 Sep 8. Osteoarthritis Cartilage. 2013. PMID: 24025318 Free PMC article.
References
-
- Alexopoulos LG, Haider MA, Vail TP, Guilak F. Alterations in the mechanical properties of the human chondrocyte pericellular matrix with osteoarthritis. J Biomech Eng. 2003;125:323–333. - PubMed
-
- Alexopoulos LG, Setton LA, Guilak F. The biomechanical role of the chondrocyte pericellular matrix in articular cartilage. Acta Biomater. 2005a;1:317–325. - PubMed
-
- Alexopoulos LG, Williams GM, Upton ML, Setton LA, Guilak F. Osteoarthritic changes in the biphasic mechanical properties of the chondrocyte pericellular matrix in articular cartilage. J Biomech. 2005b;38:509–517. - PubMed
-
- Allen DM, Mao JJ. Heterogeneous nanostructural and nanoelastic properties of pericellular and interterritorial matrices of chondrocytes by atomic force microscopy. J Struct Biol. 2004;145:196–204. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

