Odefy--from discrete to continuous models

Abstract

Background: Phenomenological information about regulatory interactions is frequently available and can be readily converted to Boolean models. Fully quantitative models, on the other hand, provide detailed insights into the precise dynamics of the underlying system. In order to connect discrete and continuous modeling approaches, methods for the conversion of Boolean systems into systems of ordinary differential equations have been developed recently. As biological interaction networks have steadily grown in size and complexity, a fully automated framework for the conversion process is desirable.

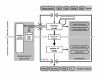
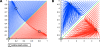
Results: We present Odefy, a MATLAB- and Octave-compatible toolbox for the automated transformation of Boolean models into systems of ordinary differential equations. Models can be created from sets of Boolean equations or graph representations of Boolean networks. Alternatively, the user can import Boolean models from the CellNetAnalyzer toolbox, GINSim and the PBN toolbox. The Boolean models are transformed to systems of ordinary differential equations by multivariate polynomial interpolation and optional application of sigmoidal Hill functions. Our toolbox contains basic simulation and visualization functionalities for both, the Boolean as well as the continuous models. For further analyses, models can be exported to SQUAD, GNA, MATLAB script files, the SB toolbox, SBML and R script files. Odefy contains a user-friendly graphical user interface for convenient access to the simulation and exporting functionalities. We illustrate the validity of our transformation approach as well as the usage and benefit of the Odefy toolbox for two biological systems: a mutual inhibitory switch known from stem cell differentiation and a regulatory network giving rise to a specific spatial expression pattern at the mid-hindbrain boundary.

Conclusions: Odefy provides an easy-to-use toolbox for the automatic conversion of Boolean models to systems of ordinary differential equations. It can be efficiently connected to a variety of input and output formats for further analysis and investigations. The toolbox is open-source and can be downloaded at http://cmb.helmholtz-muenchen.de/odefy.

Figure 1

Odefy overview. Odefy generates models from sets of Boolean equations or Boolean hypergraphs created with yEd. Alternatively, Boolean models can be imported from the CellNetAnalyzer, GINsim or the PBN toolbox. Odefy contains a method for the automatic generation of multi-compartment models from a given single cell model. Boolean models can be exported to other discrete input formats (for the GNA and SQUAD toolboxes), used for Boolean simulations and analysis within Odefy, or they can be converted to systems of ordinary differential equation (ODE). These ODE systems can either be directly simulated and analyzed with Odefy or exported to well-established model formats, including MATLAB script files, SBML, SB Toolbox models and R script files.

Figure 2

Continuous homologues of Boolean functions. Continuous homologues of Boolean functions. A Multilinear interpolation of a two-variable OR gate (Boole-Cube). B Hill functions with Hill coefficients n = 2, 4, 8, 16 and k = 0.5 as continuous relaxation of a Boolean step function. C Composition of BooleCube from (A) with Hill functions (HillCube). D normalized HillCube from (C).

Figure 3

Boolean model definition. A The easiest way to define a Boolean model in Odefy is to specify a set of Boolean equations in a text file. This example represents an asymmetric version of the mutual inhibitory switch shown in the results section. Note the use of the MATLAB language-specific operators &&, || and ~. B Regulatory interaction graph created with the yEd graph editor. Regular arrows represent activatory influences whereas diamond-head arrows stand for inhibition. Note that we need to specify a generic logic to combine multiple regulatory inputs for node E. The Odefy default at least one activator and no inhibitors logic would result in E = (A ∨ C) ˄ ¬ (B ∨ C). C Alternative representation of the Boolean model as a hypergraph. Using a specialized node '&' we can precisely specify the Boolean logic for node E. All edges not incident to a '&' node are treated with an OR logic. The resulting Boolean update rule reads E = (A ˄ ¬ B) ∨ C ∨ ¬ D. ˄ = logical AND, ∨ = logical OR, ¬ = logical NOT.

Figure 4

Odefy graphical user interface. A Screenshot of the Odefy simulation dialog for convenient access to the dynamic model parameters, initial values, conversion types and plot options. All settings can be saved to or loaded from the current workspace. B Export dialog for all discrete and continuous Odefy export formats. C Exemplary time-course simulation of the cell cycle model from [5] with default parameters.

Figure 5

Mutual inhibitory switch. A Regulatory network known to take a prominent role in stem cell differentiation processes (see e.g. [22]). It consists of two mutual inhibitory factors (here with auto-activation). Intuitively, only one of the two factors can be fully active at any given time, leading to a switch-like behavior of this circuit. B This listing diplays the set of commands required to create and analyze the OR logics version of the mutual inhibitory switch. After initializing Odefy and generating the model structure (lines 1-2), we calculate and output Boolean steady states (lines 3-4) and finally convert the model into an ODE system to generate a picture of the attractor landscape (lines 5-6). C Boolean steady states of the OR and AND version of the mutual inhibitory switch model. D, E Phase planes visualizing the attractor landscapes of the OR (D) and AND (E) logics models. The figures display trajectories of both dynamical systems from various initial concentrations. Trajectories with the same color fall into the same stable steady state. Both systems comprise three stable continuous steady states, each of which belongs to one Boolean steady state.

Figure 6

Comparison with an existing modeling study. A Phase planes visualizing the attractor landscape of the Odefy-converted AND version of the mutual inhibitory switch from various initial conditions. We set the Hill parameter n to 2 in order to represent dimer binding of transription factors as proposed in the study by Roeder et al [23]. The self-activation threshold k_s was set to 0.01, resembling a highly sensitive self-activation in comparison to the mutual inhibition. B Simulation of the ODE system from [23] with a high unspecific transription rate. We show an exact reproduction of the phase plane displayed in Figure 2(h) from the original publication. Both dynamical systems are similar in terms of multistability, steady state positions and attractor basins, i.e. the initial values that fall into a certain steady state.

Figure 7

The Mid-hindbrain boundary. A Expression patterns of four major factors at the mid-hindbrain boundary. The relevant part of the neural tube is subdivided into 6 compartments, each displaying a unique expression pattern. The right table represents the known expression patterns in a Boolean framework (note that the secreted variants of Fgf8 and Wnt1 are not included here). B This code snippet demonstrates the use of Odefy for model selection. We load a precalculated set of random models along with the 9 known valid models and iterate over all model equations (lines 1-2, mhbsettings is contained in the examples folder of the Odefy package). Next, we generate Boolean models from each equation and extend the model to a six cell multicompartment model (lines 3-4). The Boolean model is converted into a system of ODEs and simulated starting from the known expression state (lines 5-7). Note that we simulate a sufficient amount of time units to ensure the systems has fallen into a steady state. If the final state after simulation is still correct in terms of activity we assume to model to be valid (lines 8-10). C Three replicated cells from our hypothetical six-cell system. Note that Wnt1 and Fgf8 are secreted factors and exhibit their influence towards neighboring cells. D The nine network variants that give rise to the desired steady state pattern. All models contain the mutual activation between Fgf8 and Wnt1 (between neighboring cells), a mutual inhibition between Otx2 and Gbx2 as well as some regulatory incluence of the transcription factors towards the secreted factors.