(In) sensitivity to spatial distortion in natural scenes
- PMID: 20462324
- PMCID: PMC2924673
- DOI: 10.1167/10.2.23
(In) sensitivity to spatial distortion in natural scenes
Abstract
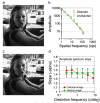
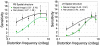
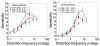
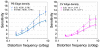
The perception of object structure in the natural environment is remarkably stable under large variation in image size and projection, especially given our insensitivity to spatial position outside the fovea. Sensitivity to periodic spatial distortions that were introduced into one quadrant of gray-scale natural images was measured in a 4AFC task. Observers were able to detect the presence of distortions in unfamiliar images even though they did not significantly affect the amplitude spectrum. Sensitivity depended on the spatial period of the distortion and on the image structure at the location of the distortion. The results suggest that the detection of distortion involves decisions made in the late stages of image perception and is based on an expectation of the typical structure of natural scenes.
Figures






References
-
- Amsler M. L’examen qualitatif de la fonctionmaculaire. Ophthalmologica. 1947;114:248–261.
-
- Anderson ND, Habak C, Wilkinson F, Wilson HR. Evaluating shape after-effects with radial frequency patterns. Vision Research. 2007;47:298–308. PubMed. - PubMed
-
- Badcock DR. Phase- or energy-based face discrimination: Some problems. Journal of Experimental Psychology of Human Perception and Performance. 1990;16:217–220. - PubMed
-
- Balboa RM, Grzywacz NM. Occlusions and their relationship with the distribution of contrasts in natural images. Vision Research. 2000;40:2661–2669. PubMed. - PubMed
-
- Barrett BT, Pacey IE, Bradley A, Thibos LN, Morrill P. Nonveridical visual perception in human amblyopia. Investigative Ophthalmology and Visual Science. 2003;44:1555–1567. [PubMed] [Article] - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

