Mutation bias favors protein folding stability in the evolution of small populations

Abstract

Mutation bias in prokaryotes varies from extreme adenine and thymine (AT) in obligatory endosymbiotic or parasitic bacteria to extreme guanine and cytosine (GC), for instance in actinobacteria. GC mutation bias deeply influences the folding stability of proteins, making proteins on the average less hydrophobic and therefore less stable with respect to unfolding but also less susceptible to misfolding and aggregation. We study a model where proteins evolve subject to selection for folding stability under given mutation bias, population size, and neutrality. We find a non-neutral regime where, for any given population size, there is an optimal mutation bias that maximizes fitness. Interestingly, this optimal GC usage is small for small populations, large for intermediate populations and around 50% for large populations. This result is robust with respect to the definition of the fitness function and to the protein structures studied. Our model suggests that small populations evolving with small GC usage eventually accumulate a significant selective advantage over populations evolving without this bias. This provides a possible explanation to the observation that most species adopting obligatory intracellular lifestyles with a consequent reduction of effective population size shifted their mutation spectrum towards AT. The model also predicts that large GC usage is optimal for intermediate population size. To test these predictions we estimated the effective population sizes of bacterial species using the optimal codon usage coefficients computed by dos Reis et al. and the synonymous to non-synonymous substitution ratio computed by Daubin and Moran. We found that the population sizes estimated in these ways are significantly smaller for species with small and large GC usage compared to species with no bias, which supports our prediction.

Figure 1. Fitness versus stabilities for (top) and (bottom).

Figure 2. Mean unfolding stability versus misfolding stability for neutrality exponent (non-neutral regime).

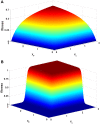
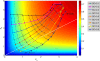
The sets of points joined with solid lines correspond to constant GC usage, between (largest ) and (largest ). grows and decreases with . The sets of points joined with dashed lines correspond to constant population size , from (smallest stability) to (largest stability). Both stability variables increase with . Data points are superimposed to a heat map of the fitness function, showing that fitness increases with . However, constant lines do not correspond to constant fitness, but there are small variations, from which the optimal GC usage is derived. The solid white line shows at which the selective pressures on and balance. One can see that, at large , is smaller than for all , so that the selective pressure is stronger on the former.

Figure 3. Fitness (in different units for each curve) versus GC usage for neutrality exponent and three different population sizes.

The curves have been shifted in the vertical direction so that their maxima coincide. We obtain by cubic fits, which are plotted as dotted, dashed, and solid lines.

Figure 4. Optimal GC usage at which the fitness is maximum versus population size .

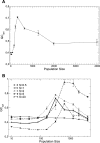
The upper plot shows data with neutrality exponent and the bottom plot shows and 20. Interpolating lines are drawn as a guide to the eye.

Figure 5. Optimal mutation bias at which the fitness is maximum versus population size for different proteins and neutrality exponent .

Upper plot: Results for individual proteins. Bottom plot: Fitness is obtained for the combination of 5 proteins either as the minimum or as the product over all proteins. Interpolating lines are drawn as a guide to the eye.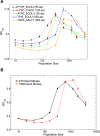

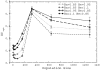
Figure 6. Optimal GC usage versus population size for neutrality exponent and different values of the neutral thresholds and , where the reference energy gap and unfolding free energy are those measured for the protein in the PDB.

We simulated all nine combinations of the values for either of . We only show four combinations since all other curves are contained between them.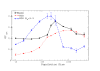

Figure 7. Comparison between the optimal GC usages computed with GKS energy parameters (dotted line and dashed line) and the BVK parameters adopted in the present study (solid line).

The conformation entropy is for BVK parameters and for GKS. The coefficient of the neutral threshold is for the dotted curve and for the dashed curve. Other parameters are fixed at , .

Figure 8. Optimal GC usage versus neutrality exponent for three population sizes .

Figure 9. Estimates of quantities correlating with effective population size obtained from genomic data.

Upper plot: Optimal codon bias estimated by dos Reis et al. versus GC content at synonymous third codon position, shown as mean and standard error of the mean for three bins of GC3 (smaller than 30%, 40 to 60%, larger than 70%). Error bars in the plot represent the standard error of the mean, and show that the mean values are significantly different. 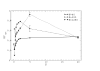However, data prior to the mean are rather broadly distributed, with standard deviations equal to (, () and (). Bottom plot: values of computed by Daubin and Moran are averaged for pairs of bacteria with low, intermediate and high GC content. Both plots support the notion that species with GC content are characterized by larger effective population size.

Figure 10. Negative correlation between misfolding and unfolding stability.

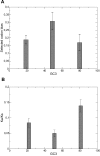
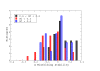
Upper plot: Simulation results for average misfolding stability versus unfolding stability for various mutation biases, three population sizes and neutrality exponent (non-neutral regime) and (neutral regime). Bottom plot: Estimated misfolding versus unfolding stability for families of homologous proteins in prokaryotic genomes (data from Ref. [12]). We distinguish genomes according to content at third codon position. The solid line represents a linear fit of misfolding stability for genomes with moderate or no mutation bias ().

Figure 11. Relationship between GC usage and protein folding stability in orthologous proteins in different prokaryotic genomes (data taken from Ref. [12]).

Histogram of the difference between the actual misfolding stability and the misfolding stability expected from the unfolding stability, using the relationship derived from species with moderate bias (continuous line in the previous plot). Notice that species with small and large GC usage have smaller than expected misfolding stability.