Viral phylodynamics and the search for an 'effective number of infections'
- PMID: 20478883
- PMCID: PMC2880113
- DOI: 10.1098/rstb.2010.0060
Viral phylodynamics and the search for an 'effective number of infections'
Abstract
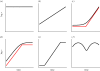
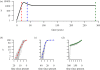
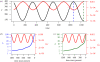
Information on the dynamics of the effective population size over time can be obtained from the analysis of phylogenies, through the application of time-varying coalescent models. This approach has been used to study the dynamics of many different viruses, and has demonstrated a wide variety of patterns, which have been interpreted in the context of changes over time in the 'effective number of infections', a quantity proportional to the number of infected individuals. However, for infectious diseases, the rate of coalescence is driven primarily by new transmissions i.e. the incidence, and only indirectly by the number of infected individuals through sampling effects. Using commonly used epidemiological models, we show that the coalescence rate may indeed reflect the number of infected individuals during the initial phase of exponential growth when time is scaled by infectivity, but in general, a single change in time scale cannot be used to estimate the number of infected individuals. This has important implications when integrating phylogenetic data in the context of other epidemiological data.
Figures
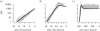
References
-
- Amore G., Bertolotti L., Hamer G., Kitron U., Walker E., Ruiz M., Brawn J., Goldberg T.In press Multi-year evolutionary dynamics of West Nile virus 1 in suburban Chicago, USA, 2005–2007. Phil. Trans. R. Soc. Lond. B 365, 1871–1878 (doi:10.1098/rstb.2010.0054) - DOI - PMC - PubMed
-
- Baillie G. J., Kolokotronis S.-O., Waltari E., Maffei J. G., Kramer L. D., Perkins S. L.2008Phylogenetic and evolutionary analyses of St Louis encephalitis virus genomes. Mol. Phylogenet. Evol. 47, 717–728 (doi:10.1016/j.ympev.2008.02.015) - DOI - PubMed
-
- Bello G., Eyer-Silva W. A., Couto-Fernandez J. C., Guimarães M. L., Chequer-Fernandez S. L., Teixeira S. L. M., Morgado M. G.2007Demographic history of HIV-1 subtypes B and F in Brazil. Infect. Genet. Evol., 7, 263–270 (doi:10.1016/j.meegid.2006.11.002) - DOI - PubMed
-
- Bello G., Guimarães M. L., Passaes C. P. B., Almeida S. E. M., Veloso V. G., Morgado M. G.2009Short communication: evidences of recent decline in the expansion rate of the HIV type 1 subtype C and CRF31_BC epidemics in southern Brazil. AIDS Res. Hum. Retroviruses 25, 1065–1069 (doi:10.1089/aid.2009.0106) - DOI - PubMed
-
- Bennett S. N., Drummond A. J., Kapan D. D., Suchard M. A., Muñoz-Jordán J. L., Pybus O. G., Holmes E. C., Gubler D. J.2009Epidemic dynamics revealed in dengue evolution. Mol. Biol. Evol. 27, 811–818 (doi:10.1093/molbev/msp285) - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

