Dynamics of bacterial swarming
- PMID: 20483315
- PMCID: PMC2872219
- DOI: 10.1016/j.bpj.2010.01.053
Dynamics of bacterial swarming
Abstract
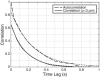
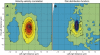
When vegetative bacteria that can swim are grown in a rich medium on an agar surface, they become multinucleate, elongate, synthesize large numbers of flagella, produce wetting agents, and move across the surface in coordinated packs: they swarm. We examined the motion of swarming Escherichia coli, comparing the motion of individual cells to their motion during swimming. Swarming cells' speeds are comparable to bulk swimming speeds, but very broadly distributed. Their speeds and orientations are correlated over a short distance (several cell lengths), but this correlation is not isotropic. We observe the swirling that is conspicuous in many swarming systems, probably due to increasingly long-lived correlations among cells that associate into groups. The normal run-tumble behavior seen in swimming chemotaxis is largely suppressed, instead, cells are continually reoriented by random jostling by their neighbors, randomizing their directions in a few tenths of a second. At the edge of the swarm, cells often pause, then swim back toward the center of the swarm or along its edge. Local alignment among cells, a necessary condition of many flocking theories, is accomplished by cell body collisions and/or short-range hydrodynamic interactions.
Copyright 2010 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures

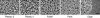
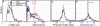
Similar articles
-
Tumble Suppression Is a Conserved Feature of Swarming Motility.mBio. 2020 Jun 16;11(3):e01189-20. doi: 10.1128/mBio.01189-20. mBio. 2020. PMID: 32546625 Free PMC article.
-
Visualization of Flagella during bacterial Swarming.J Bacteriol. 2010 Jul;192(13):3259-67. doi: 10.1128/JB.00083-10. Epub 2010 Apr 2. J Bacteriol. 2010. PMID: 20363932 Free PMC article.
-
Escherichia coli Remodels the Chemotaxis Pathway for Swarming.mBio. 2019 Mar 19;10(2):e00316-19. doi: 10.1128/mBio.00316-19. mBio. 2019. PMID: 30890609 Free PMC article.
-
Swarming: flexible roaming plans.J Bacteriol. 2013 Mar;195(5):909-18. doi: 10.1128/JB.02063-12. Epub 2012 Dec 21. J Bacteriol. 2013. PMID: 23264580 Free PMC article. Review.
-
Shelter in a Swarm.J Mol Biol. 2015 Nov 20;427(23):3683-94. doi: 10.1016/j.jmb.2015.07.025. Epub 2015 Aug 12. J Mol Biol. 2015. PMID: 26277623 Free PMC article. Review.
Cited by
-
Bacterial Motility and Its Role in Skin and Wound Infections.Int J Mol Sci. 2023 Jan 15;24(2):1707. doi: 10.3390/ijms24021707. Int J Mol Sci. 2023. PMID: 36675220 Free PMC article. Review.
-
The 3D architecture of a bacterial swarm has implications for antibiotic tolerance.Sci Rep. 2018 Oct 25;8(1):15823. doi: 10.1038/s41598-018-34192-2. Sci Rep. 2018. PMID: 30361680 Free PMC article.
-
A multiphase theory for spreading microbial swarms and films.Elife. 2019 Apr 30;8:e42697. doi: 10.7554/eLife.42697. Elife. 2019. PMID: 31038122 Free PMC article.
-
Multiple functions of flagellar motility and chemotaxis in bacterial physiology.FEMS Microbiol Rev. 2021 Nov 23;45(6):fuab038. doi: 10.1093/femsre/fuab038. FEMS Microbiol Rev. 2021. PMID: 34227665 Free PMC article. Review.
-
Decoding Bacterial Motility: From Swimming States to Patterns and Chemotactic Strategies.Biomolecules. 2025 Jan 23;15(2):170. doi: 10.3390/biom15020170. Biomolecules. 2025. PMID: 40001473 Free PMC article. Review.
References
-
- Berg H.C., Anderson R.A. Bacteria swim by rotating their flagellar filaments. Nature. 1973;245:380–382. - PubMed
-
- Berg H.C. Springer; New York: 2004. E. coli in Motion.
-
- Baker M.A.B., Berry R.M. An introduction to the physics of the bacterial flagellar motor: a nanoscale rotary electric motor. Contemp. Phys. 2009;50:617–632.
-
- Sowa Y., Berry R.M. Bacterial flagellar motor. Q. Rev. Biophys. 2008;41:103–132. - PubMed
-
- Terashima H., Kojima S., Homma M. Flagellar motility in bacteria structure and function of flagellar motor. Int. Rev. Cell Mol. Biol. 2008;270:39–85. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

