Elasticity in ionically cross-linked neurofilament networks

Abstract

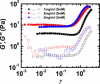
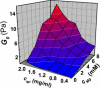
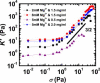
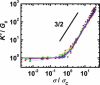
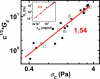
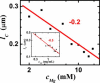
Neurofilaments are found in abundance in the cytoskeleton of neurons, where they act as an intracellular framework protecting the neuron from external stresses. To elucidate the nature of the mechanical properties that provide this protection, we measure the linear and nonlinear viscoelastic properties of networks of neurofilaments. These networks are soft solids that exhibit dramatic strain stiffening above critical strains of 30-70%. Surprisingly, divalent ions such as Mg(2+), Ca(2+), and Zn(2+) act as effective cross-linkers for neurofilament networks, controlling their solidlike elastic response. This behavior is comparable to that of actin-binding proteins in reconstituted filamentous actin. We show that the elasticity of neurofilament networks is entropic in origin and is consistent with a model for cross-linked semiflexible networks, which we use to quantify the cross-linking by divalent ions.

Figure 1

The frequency dependence of the linear viscoelastic moduli of cross-linked networks for a variety of NF and Mg²⁺ concentrations. (A) Variations of the moduli at constant Mg²⁺ concentration (5 mM) and changing filament concentration. (B) Variations of the moduli at constant NF concentration (1.5 mg/ml) and changing Mg²⁺ concentration.

Figure 2

The strain-stiffening behavior of NF networks at various Mg²⁺ and NF concentrations. G′ is the elastic modulus (solid squares) and G″ the viscous modulus (open squares). Dramatic nonlinearities are seen at critical strains ranging from 30% to 70%.

Figure 3

The linear elastic modulus, G₀, as a function of c_NF and c_Mg. The network elasticity can be finely tuned over an order of magnitude by varying the concentration of the cross-linker Mg²⁺ and the NF concentration. The essential role of Mg²⁺ as a network cross-linker is evinced by the markedly stronger dependence on c_NF for increasing divalent ion concentration.

Figure 4

The dependence of K′(σ) on σ for a variety of NF and Mg²⁺ concentrations. The effects of varying c_Mg at a constant filament concentration of 1.5 mg/ml and c_NF at a constant divalent ion concentration of 5 mM are shown. As expected, the linear elastic modulus and the breakage stress differ; however, all data show an exponent of ∼3/2 (black line), in agreement with the affine thermal model.

Figure 5

Collapse of all data sets of the σ dependence of K′ onto a single universal curve. The scaling parameters are G₀, the linear elastic modulus, and σ_c, the critical stress. These parameters are calculated using a least-squares regression. Data shown represent varying filament concentrations from 0.5 to 2.2 mg/ml and varying divalent ion concentrations from 2 to 8 mM. The data points at the high-stress end that show a downturn just before network failure are likely due to network breakage and are therefore removed to avoid improper influence on regression parameters.

Figure 6

The dependence of c_NF^1/2G₀ on σ_c. The solid line is the result of a regression fit to the data and depicts an exponent of 1.54. This is in agreement with the affine thermal model, which predicts an exponent of 3/2. Data were obtained for Mg²⁺ (solid squares), Ca²⁺ (open squares), and Zn²⁺ (crossed squares). (Inset) Dependence of G₀ on c_NF. An exponent of 2.5 was obtained from regression. This is also consistent with the affine thermal model, which predicts an exponent of 2.2.

Figure 7

Dependence of l_c on c_NF at a fixed molar ratio of 1000. The solid line is the result of a regression fit and exhibits an exponent of −0.5. This is consistent with the affine thermal model, which predicts an exponent of −2/5. (Inset) Dependence of l_c on c_Mg at a fixed filament concentration, with an exponent of −0.2 obtained by a regression fit.