Impact of dendritic size and dendritic topology on burst firing in pyramidal cells
- PMID: 20485556
- PMCID: PMC2869305
- DOI: 10.1371/journal.pcbi.1000781
Impact of dendritic size and dendritic topology on burst firing in pyramidal cells
Abstract
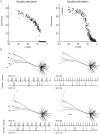
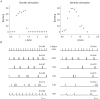
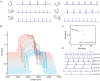
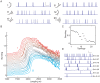
Neurons display a wide range of intrinsic firing patterns. A particularly relevant pattern for neuronal signaling and synaptic plasticity is burst firing, the generation of clusters of action potentials with short interspike intervals. Besides ion-channel composition, dendritic morphology appears to be an important factor modulating firing pattern. However, the underlying mechanisms are poorly understood, and the impact of morphology on burst firing remains insufficiently known. Dendritic morphology is not fixed but can undergo significant changes in many pathological conditions. Using computational models of neocortical pyramidal cells, we here show that not only the total length of the apical dendrite but also the topological structure of its branching pattern markedly influences inter- and intraburst spike intervals and even determines whether or not a cell exhibits burst firing. We found that there is only a range of dendritic sizes that supports burst firing, and that this range is modulated by dendritic topology. Either reducing or enlarging the dendritic tree, or merely modifying its topological structure without changing total dendritic length, can transform a cell's firing pattern from bursting to tonic firing. Interestingly, the results are largely independent of whether the cells are stimulated by current injection at the soma or by synapses distributed over the dendritic tree. By means of a novel measure called mean electrotonic path length, we show that the influence of dendritic morphology on burst firing is attributable to the effect both dendritic size and dendritic topology have, not on somatic input conductance, but on the average spatial extent of the dendritic tree and the spatiotemporal dynamics of the dendritic membrane potential. Our results suggest that alterations in size or topology of pyramidal cell morphology, such as observed in Alzheimer's disease, mental retardation, epilepsy, and chronic stress, could change neuronal burst firing and thus ultimately affect information processing and cognition.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures



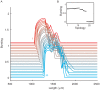

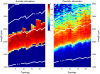


References
-
- Llinás RR. The intrinsic electrophysiological properties of mammalian neurons: insights into central nervous system function. Science. 1988;242:1654–1664. - PubMed
-
- Connors BW, Gutnick MJ. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 1990;13:99–104. - PubMed
-
- Contreras D. Electrophysiological classes of neocortical neurons. Neural Networks. 2004;17:633–646. - PubMed
-
- Krahe R, Gabbiani F. Burst firing in sensory systems. Nature Reviews Neuroscience. 2004;5:13–23. - PubMed
-
- Eggermont JJ, Smith GM. Burst-firing sharpens frequency-tuning in primary auditory cortex. Neuroreport. 1996;7:753–757. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

