Thermodynamic and kinetic considerations for the reaction of semiquinone radicals to form superoxide and hydrogen peroxide
- PMID: 20493944
- PMCID: PMC2936108
- DOI: 10.1016/j.freeradbiomed.2010.05.009
Thermodynamic and kinetic considerations for the reaction of semiquinone radicals to form superoxide and hydrogen peroxide
Abstract
The quinone/semiquinone/hydroquinone triad (Q/SQ(*-)/H(2)Q) represents a class of compounds that has great importance in a wide range of biological processes. The half-cell reduction potentials of these redox couples in aqueous solutions at neutral pH, E degrees ', provide a window to understanding the thermodynamic and kinetic characteristics of this triad and their associated chemistry and biochemistry in vivo. Substituents on the quinone ring can significantly influence the electron density "on the ring" and thus modify E degrees' dramatically. E degrees' of the quinone governs the reaction of semiquinone with dioxygen to form superoxide. At near-neutral pH the pK(a)'s of the hydroquinone are outstanding indicators of the electron density in the aromatic ring of the members of these triads (electrophilicity) and thus are excellent tools to predict half-cell reduction potentials for both the one-electron and two-electron couples, which in turn allow estimates of rate constants for the reactions of these triads. For example, the higher the pK(a)'s of H(2)Q, the lower the reduction potentials and the higher the rate constants for the reaction of SQ(*-) with dioxygen to form superoxide. However, hydroquinone autoxidation is controlled by the concentration of di-ionized hydroquinone; thus, the lower the pK(a)'s the less stable H(2)Q to autoxidation. Catalysts, e.g., metals and quinone, can accelerate oxidation processes; by removing superoxide and increasing the rate of formation of quinone, superoxide dismutase can accelerate oxidation of hydroquinones and thereby increase the flux of hydrogen peroxide. The principal reactions of quinones are with nucleophiles via Michael addition, for example, with thiols and amines. The rate constants for these addition reactions are also related to E degrees'. Thus, pK(a)'s of a hydroquinone and E degrees ' are central to the chemistry of these triads.
Copyright 2010 Elsevier Inc. All rights reserved.
Figures

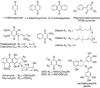





 , blue) are the first pKa of a particular hydroquinone; the diamonds (◆, black) are the second pKa of the hydroquinone; pKa's are from [11,12,39]. The para-quinones/hydroquinones a–m show a linear relationship between the one-electron reduction potential of the quinone (E°′(Q/SQ•−)) and the first and second pKa's of the corresponding hydroquinone. The one-electron reduction potentials for quinones k and l have been estimated from Fig. 4; compounds A (catechol) and B (tetrachloro-1,4-hydroquinone) are not included in the linear regression of the two lines. We anticipate that ortho-hydroquinones would behave similarly to para-hydroquinones, but there would most likely be a systematic offset relative to the plots for para-hydroquinones. (A note on tetrachloro-1,4-hydroquinone: E°′(Q/SQ•−) for tetrachloro-1,4-hydroquinone (B) has been estimated from the correlation of the reduction potentials determined in methyl cyanide [40,78]; knowing that pKa1 for tetrachloro-1,4-hydroquinone is 5.6 [12] suggests that the one-electron reduction potential is actually about +800 mV in aqueous solution.) The compounds are: a. ubiquionol-1, coenzyme Q-1; b, tetramethyl-1,4-hydroquinone; c, 2,3,5-trimethyl-1,4-hydroquinone; d, plastoquinol-1; e, 2,6-dimethyl-1,4-hydroquinone; f, 2-methyl-5-isopropyl-1,4-hydroquinone; g, 2,3-dimethyl-1,4-hydroquinone; h, 2,5-dimethyl-1,4-hydroquinone; i, 2-methyl-1,4-hydroquinone; j, 1,4-hydroquinone; k, 2-chloro-1,4-hydroquinone; l, 2,6-dichloro-1,4-hydroquinone; m, 2,5-dichloro-1,4-hydroquinone; A, catechol; B, tetrachloro-1,4-hydroquinone.
, blue) are the first pKa of a particular hydroquinone; the diamonds (◆, black) are the second pKa of the hydroquinone; pKa's are from [11,12,39]. The para-quinones/hydroquinones a–m show a linear relationship between the one-electron reduction potential of the quinone (E°′(Q/SQ•−)) and the first and second pKa's of the corresponding hydroquinone. The one-electron reduction potentials for quinones k and l have been estimated from Fig. 4; compounds A (catechol) and B (tetrachloro-1,4-hydroquinone) are not included in the linear regression of the two lines. We anticipate that ortho-hydroquinones would behave similarly to para-hydroquinones, but there would most likely be a systematic offset relative to the plots for para-hydroquinones. (A note on tetrachloro-1,4-hydroquinone: E°′(Q/SQ•−) for tetrachloro-1,4-hydroquinone (B) has been estimated from the correlation of the reduction potentials determined in methyl cyanide [40,78]; knowing that pKa1 for tetrachloro-1,4-hydroquinone is 5.6 [12] suggests that the one-electron reduction potential is actually about +800 mV in aqueous solution.) The compounds are: a. ubiquionol-1, coenzyme Q-1; b, tetramethyl-1,4-hydroquinone; c, 2,3,5-trimethyl-1,4-hydroquinone; d, plastoquinol-1; e, 2,6-dimethyl-1,4-hydroquinone; f, 2-methyl-5-isopropyl-1,4-hydroquinone; g, 2,3-dimethyl-1,4-hydroquinone; h, 2,5-dimethyl-1,4-hydroquinone; i, 2-methyl-1,4-hydroquinone; j, 1,4-hydroquinone; k, 2-chloro-1,4-hydroquinone; l, 2,6-dichloro-1,4-hydroquinone; m, 2,5-dichloro-1,4-hydroquinone; A, catechol; B, tetrachloro-1,4-hydroquinone.





Similar articles
-
Hydroquinone-Mediated Redox Cycling of Iron and Concomitant Oxidation of Hydroquinone in Oxic Waters under Acidic Conditions: Comparison with Iron-Natural Organic Matter Interactions.Environ Sci Technol. 2015 Dec 15;49(24):14076-84. doi: 10.1021/acs.est.5b03189. Epub 2015 Dec 2. Environ Sci Technol. 2015. PMID: 26579728
-
Kinetics and mechanism of auto- and copper-catalyzed oxidation of 1,4-naphthohydroquinone.Free Radic Biol Med. 2014 Jun;71:291-302. doi: 10.1016/j.freeradbiomed.2014.03.021. Epub 2014 Mar 27. Free Radic Biol Med. 2014. PMID: 24681336
-
Thiol oxidation coupled to DT-diaphorase-catalysed reduction of diaziquone. Reductive and oxidative pathways of diaziquone semiquinone modulated by glutathione and superoxide dismutase.Biochem J. 1992 Sep 1;286 ( Pt 2)(Pt 2):481-90. doi: 10.1042/bj2860481. Biochem J. 1992. PMID: 1530580 Free PMC article.
-
The metabolism of quinone-containing alkylating agents: free radical production and measurement.Front Biosci. 2000 Jul 1;5:D629-38. doi: 10.2741/gutier. Front Biosci. 2000. PMID: 10877994 Review.
-
Multiple actions of superoxide dismutase: why can it both inhibit and stimulate reduction of oxygen by hydroquinones?Free Radic Biol Med. 1990;9(2):143-8. doi: 10.1016/0891-5849(90)90117-2. Free Radic Biol Med. 1990. PMID: 2227529 Review.
Cited by
-
Glycation of bovine serum albumin by ascorbate in vitro: Possible contribution of the ascorbyl radical?Redox Biol. 2015 Dec;6:93-99. doi: 10.1016/j.redox.2015.06.017. Epub 2015 Jul 2. Redox Biol. 2015. PMID: 26202868 Free PMC article.
-
Juglone, a plant-derived 1,4-naphthoquinone, binds to hydroxylamine oxidoreductase and inhibits the electron transfer to cytochrome c554.Appl Environ Microbiol. 2023 Dec 21;89(12):e0129123. doi: 10.1128/aem.01291-23. Epub 2023 Nov 27. Appl Environ Microbiol. 2023. PMID: 38009977 Free PMC article.
-
Unexpected Heme Redox Potential Values Implicate an Uphill Step in Cytochrome b6f.J Phys Chem B. 2022 Dec 1;126(47):9771-9780. doi: 10.1021/acs.jpcb.2c05729. Epub 2022 Nov 18. J Phys Chem B. 2022. PMID: 36399615 Free PMC article.
-
Oxidation of 3,4-dihydroxyphenylacetaldehyde, a toxic dopaminergic metabolite, to a semiquinone radical and an ortho-quinone.J Biol Chem. 2011 Jul 29;286(30):26978-86. doi: 10.1074/jbc.M111.249532. Epub 2011 Jun 3. J Biol Chem. 2011. PMID: 21642436 Free PMC article.
-
Naphthoquinones Oxidize H2S to Polysulfides and Thiosulfate, Implications for Therapeutic Applications.Int J Mol Sci. 2022 Oct 31;23(21):13293. doi: 10.3390/ijms232113293. Int J Mol Sci. 2022. PMID: 36362080 Free PMC article.
References
-
- Krueger FR, Werther W, Kissel J, Schmidt ER. Assignment of quinone derivatives as the main compound class composing ‘interstellar’ grains based on both polarity ions detected by the ‘Cometary and Interstellar Dust Analyser’ (CIDA) onboard the spacecraft STARDUST. Rapid Commun. Mass Spectrom. 2004;18:103–111. - PubMed
-
- Trumpower BL. The protonmotive Q cycle. Energy transduction by coupling of proton translocation to electron transfer by the cytochrome bc1 complex. J. Biol. Chem. 1990;265:11409–11412. - PubMed
-
- Tiemann R, Renger G, Gräber P, Witt HT. The plastoquinone pool as possible hydrogen pump in photosynthesis. Biochim. Biophys. Acta. 1979;546:498–519. - PubMed
-
- Odom AL, Hatwig CA, Stanley JS, Benson AM. Biochemical determinants of Adriamycin toxicity in mouse liver, heart and intestine. Biochem. Pharmacol. 1992;43(4):831–836. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

