Evolution towards oscillation or stability in a predator-prey system
- PMID: 20504808
- PMCID: PMC2982064
- DOI: 10.1098/rspb.2010.0691
Evolution towards oscillation or stability in a predator-prey system
Abstract
We studied a prey-predator system in which both species evolve. We discuss here the conditions that result in coevolution towards a stable equilibrium or towards oscillations. First, we show that a stable equilibrium or population oscillations with small amplitude is likely to occur if the prey's (host's) defence is effective when compared with the predator's (parasite's) attacking ability at equilibrium, whereas large-amplitude oscillations are likely if the predator's (parasite's) attacking ability exceeds the prey's (host's) defensive ability. Second, a stable equilibrium is more likely if the prey's defensive trait evolves faster than the predator's attack trait, whereas population oscillations are likely if the predator's trait evolves faster than that of the prey. Third, when the adaptation rates of both species are similar, the amplitude of the fluctuations in their abundances is small when the adaptation rate is either very slow or very fast, but at an intermediate rate of adaptation the fluctuations have a large amplitude. We also show the case in which the prey's abundance and trait fluctuate greatly, while those of the predator remain almost unchanged. Our results predict that populations and traits in host-parasite systems are more likely than those in prey-predator systems to show large-amplitude oscillations.
Figures
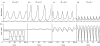
 . The solid and dotted lines indicate the dynamics of the prey and predator, respectively. The inset in the lower panel of (a) enlarges a portion of panel. The parameter values are ρX = ρY = 2, r0 = 1, g0 = 1, a0 = 3, θ = 20 and d = 0.3. The initial values are (X, Y, u, v) = (1, 0.5, 0.1, 0.1).
. The solid and dotted lines indicate the dynamics of the prey and predator, respectively. The inset in the lower panel of (a) enlarges a portion of panel. The parameter values are ρX = ρY = 2, r0 = 1, g0 = 1, a0 = 3, θ = 20 and d = 0.3. The initial values are (X, Y, u, v) = (1, 0.5, 0.1, 0.1).
 and
and  . We adopted the linear functions r = r0(1−ρXu) and g = g0(1−ρYv). The white and shaded regions indicate the parameter ranges in which the equilibrium is stable and unstable, respectively. (a) u* = v*. We assumed ρX = ρY=2. (b) u* < v*. The shaded region is the unstable region when ρX = 1.98 and ρY = 2. The ordered pairs show (ρX, ρY), corresponding to each boundary (dotted lines) between stable and unstable regions, with the region on the left side of the boundary unstable and the one on the right stable. The other parameter values are r0 = 1, g0 = 1, a0 = 3, θ = 20 and d = 0.2.
. We adopted the linear functions r = r0(1−ρXu) and g = g0(1−ρYv). The white and shaded regions indicate the parameter ranges in which the equilibrium is stable and unstable, respectively. (a) u* = v*. We assumed ρX = ρY=2. (b) u* < v*. The shaded region is the unstable region when ρX = 1.98 and ρY = 2. The ordered pairs show (ρX, ρY), corresponding to each boundary (dotted lines) between stable and unstable regions, with the region on the left side of the boundary unstable and the one on the right stable. The other parameter values are r0 = 1, g0 = 1, a0 = 3, θ = 20 and d = 0.2.

Similar articles
-
Unique coevolutionary dynamics in a predator-prey system.J Theor Biol. 2011 May 21;277(1):83-9. doi: 10.1016/j.jtbi.2011.02.015. Epub 2011 Feb 24. J Theor Biol. 2011. PMID: 21354181
-
Coevolution in a one predator-two prey system.PLoS One. 2010 Nov 9;5(11):e13887. doi: 10.1371/journal.pone.0013887. PLoS One. 2010. PMID: 21085473 Free PMC article.
-
PREY ADAPTATION AS A CAUSE OF PREDATOR-PREY CYCLES.Evolution. 1997 Dec;51(6):1742-1750. doi: 10.1111/j.1558-5646.1997.tb05098.x. Evolution. 1997. PMID: 28565102
-
The subcritical collapse of predator populations in discrete-time predator-prey models.Math Biosci. 1992 Jun;110(1):45-66. doi: 10.1016/0025-5564(92)90014-n. Math Biosci. 1992. PMID: 1623297 Review.
-
Outrun or Outmaneuver: Predator-Prey Interactions as a Model System for Integrating Biomechanical Studies in a Broader Ecological and Evolutionary Context.Integr Comp Biol. 2015 Dec;55(6):1188-97. doi: 10.1093/icb/icv074. Epub 2015 Jun 27. Integr Comp Biol. 2015. PMID: 26117833 Review.
Cited by
-
Rapid evolution of prey maintains predator diversity.PLoS One. 2019 Dec 31;14(12):e0227111. doi: 10.1371/journal.pone.0227111. eCollection 2019. PLoS One. 2019. PMID: 31891629 Free PMC article.
-
Natural selection contributes to food web stability.PLoS One. 2020 Jan 10;15(1):e0227420. doi: 10.1371/journal.pone.0227420. eCollection 2020. PLoS One. 2020. PMID: 31923285 Free PMC article.
-
Character displacement or priority effects: immigration timing can affect community assembly with rapid evolution.Proc Biol Sci. 2024 Nov;291(2035):20242145. doi: 10.1098/rspb.2024.2145. Epub 2024 Nov 20. Proc Biol Sci. 2024. PMID: 39561793 Free PMC article.
-
Non-genetic inheritance and the patterns of antagonistic coevolution.BMC Evol Biol. 2012 Jun 21;12:93. doi: 10.1186/1471-2148-12-93. BMC Evol Biol. 2012. PMID: 22720868 Free PMC article.
-
Antagonistic coevolution between quantitative and Mendelian traits.Proc Biol Sci. 2016 Mar 30;283(1827):20152926. doi: 10.1098/rspb.2015.2926. Proc Biol Sci. 2016. PMID: 27009218 Free PMC article.
References
-
- Abrams P. A.2000The evolution of predator-prey interactions: theory and evidence. Annu. Rev. Ecol. Syst. 31, 79–105 (doi:10.1146/annurev.ecolsys.31.1.79) - DOI
-
- Abrams P. A., Matsuda H.1997Fitness minimization and dynamic instability as a consequence of predator–prey coevolution. Evol. Ecol. 11, 1–20 (doi:10.1023/A:1018445517101) - DOI
-
- Abrams P. A., Harada Y., Matsuda H.1993Unstable fitness maxima and stable fitness minima in the evolution of continuous traits. Evol. Ecol. 7, 465–487 (doi:10.1007/BF01237642) - DOI
-
- Agashe D.2009The stabilizing effect of intraspecific genetic variation on population dynamics in novel and ancestral habitats. Am. Nat. 174, 255–267 (doi:10.1086/600085) - DOI - PubMed
-
- Agrawal A. A.2001Phenotypic plasticity in the interactions and evolution of species. Science 294, 321–326 (doi:10.1126/science.1060701) - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

