A conceptual cellular interaction model of left ventricular remodelling post-MI: dynamic network with exit-entry competition strategy
- PMID: 20522255
- PMCID: PMC2880411
- DOI: 10.1186/1752-0509-4-S1-S5
A conceptual cellular interaction model of left ventricular remodelling post-MI: dynamic network with exit-entry competition strategy
Abstract
Background: Progressive remodelling of the left ventricle (LV) following myocardial infarction (MI) is an outcome of spatial-temporal cellular interactions among different cell types that leads to heart failure for a significant number of patients. Cellular populations demonstrate temporal profiles of flux post-MI. However, little is known about the relationship between cell populations and the interaction strength among cells post-MI. The objective of this study was to establish a conceptual cellular interaction model based on a recently established graph network to describe the interaction between two types of cells.
Results: We performed stability analysis to investigate the effects of the interaction strengths, the initial status, and the number of links between cells on the cellular population in the dynamic network. Our analysis generated a set of conditions on interaction strength, structure of the network, and initial status of the network to predict the evolutionary profiles of the network. Computer simulations of our conceptual model verified our analysis.
Conclusions: Our study introduces a dynamic network to model cellular interactions between two different cell types which can be used to model the cellular population changes post-MI. The results on stability analysis can be used as a tool to predict the responses of particular cell populations.
Figures
 , or a type C cell with probability of
, or a type C cell with probability of  according to the exit-entry evolutionary strategy, which is shown in the right part of Figure 1 (Right).
according to the exit-entry evolutionary strategy, which is shown in the right part of Figure 1 (Right).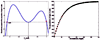



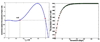


References
-
- Cohn JN, Ferrari R, Sharpe N. Cardiac remodeling--concepts and clinical implications: a consensus paper from an international forum on cardiac remodeling. Behalf of an International Forum on Cardiac Remodeling. J Am Coll Cardiol. 2000;35(3):569–582. doi: 10.1016/S0735-1097(99)00630-0. - DOI - PubMed
-
- Pfeffer MA, Braunwald E. Ventricular Remodeling After Myocardial Infarction. Experimental observations and clinical implications. Circulation. 1990;81:1161–1172. - PubMed
-
- Lindsey M, Escobar GP, Dobrucki WL, Goshorn KD, Bouges S, Mingoia TJ, McClister MD, Su, Jr. H, Gannon J, MacGillivray C, Lee TR, Sinusas JA. Matrix metalloproteinase-9 gene deletion facilitates angiogenesis after myocardial infarction. Am J Physiol Heart Circ Physiol 2006. 2006;290():H232–H239. doi: 10.1016/S0735-1097(99)00630-0. - DOI - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Medical

