Game theory of social distancing in response to an epidemic
- PMID: 20523740
- PMCID: PMC2877723
- DOI: 10.1371/journal.pcbi.1000793
Game theory of social distancing in response to an epidemic
Abstract
Social distancing practices are changes in behavior that prevent disease transmission by reducing contact rates between susceptible individuals and infected individuals who may transmit the disease. Social distancing practices can reduce the severity of an epidemic, but the benefits of social distancing depend on the extent to which it is used by individuals. Individuals are sometimes reluctant to pay the costs inherent in social distancing, and this can limit its effectiveness as a control measure. This paper formulates a differential-game to identify how individuals would best use social distancing and related self-protective behaviors during an epidemic. The epidemic is described by a simple, well-mixed ordinary differential equation model. We use the differential game to study potential value of social distancing as a mitigation measure by calculating the equilibrium behaviors under a variety of cost-functions. Numerical methods are used to calculate the total costs of an epidemic under equilibrium behaviors as a function of the time to mass vaccination, following epidemic identification. The key parameters in the analysis are the basic reproduction number and the baseline efficiency of social distancing. The results show that social distancing is most beneficial to individuals for basic reproduction numbers around 2. In the absence of vaccination or other intervention measures, optimal social distancing never recovers more than 30% of the cost of infection. We also show how the window of opportunity for vaccine development lengthens as the efficiency of social distancing and detection improve.
Conflict of interest statement
The author has declared that no competing interests exist.
Figures
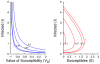
 (left) and transformed to explicit coordinates
(left) and transformed to explicit coordinates  (right) for the infinite-horizon problem with maximum efficiency
(right) for the infinite-horizon problem with maximum efficiency  . The greater the value of the susceptible state (
. The greater the value of the susceptible state ( ), the greater the instantaneous social distancing. We find that increasing the number of susceptible individuals always decreases the investment in social distancing, and the greatest investments in social distancing occur when the smallest part of the population is susceptible. Note that in the dimensionless model, the value of the infection state
), the greater the instantaneous social distancing. We find that increasing the number of susceptible individuals always decreases the investment in social distancing, and the greatest investments in social distancing occur when the smallest part of the population is susceptible. Note that in the dimensionless model, the value of the infection state  .
.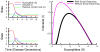
 ,
,  ). In the phase plane (right), we see that both epidemics track each other perfectly until
). In the phase plane (right), we see that both epidemics track each other perfectly until  , when individuals begin to use social distancing to reduce transmission. Eventually, social distancing leads to a smaller epidemic. The convexity change appearing at the bottom the phaseplane orbit with social distancing corresponds to the cessation of social distancing.
, when individuals begin to use social distancing to reduce transmission. Eventually, social distancing leads to a smaller epidemic. The convexity change appearing at the bottom the phaseplane orbit with social distancing corresponds to the cessation of social distancing.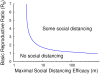
 and the maximum efficiency
and the maximum efficiency  , and is independent of the exact form of
, and is independent of the exact form of  . As rough rules of thumb, if
. As rough rules of thumb, if  or
or  , then equilibrium behavior involves no social distancing.
, then equilibrium behavior involves no social distancing.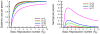
 (left) under equilibrium social distancing for the infinite-horizon problem with several efficiencies
(left) under equilibrium social distancing for the infinite-horizon problem with several efficiencies  under Eq. (6), and the corresponding per-capita savings (right). Savings in expected cost compared to universal abstention from social distancing are largest for moderate basic reproduction numbers, but are relatively small, even in the limit of infinitely efficient social distancing. The
under Eq. (6), and the corresponding per-capita savings (right). Savings in expected cost compared to universal abstention from social distancing are largest for moderate basic reproduction numbers, but are relatively small, even in the limit of infinitely efficient social distancing. The  case corresponds to infection of the minimum number of people necessary to reduce the reproduction ratio below
case corresponds to infection of the minimum number of people necessary to reduce the reproduction ratio below  .
.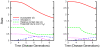
 generations (left) and
generations (left) and  generations (right) after the start of the epidemic. Investments in social distancing begin well after the start of the epidemic but continue right up to the time of vaccination. Social distancing begins sooner when vaccine development is faster. For these parameter values (
generations (right) after the start of the epidemic. Investments in social distancing begin well after the start of the epidemic but continue right up to the time of vaccination. Social distancing begins sooner when vaccine development is faster. For these parameter values ( ), individuals save
), individuals save  % of the cost of infection per capita (left) and
% of the cost of infection per capita (left) and  % of the cost of infection (right).
% of the cost of infection (right).
 ) depend on the delay between the start of social-distancing practices and the date when mass-vaccination becomes universally available if individuals use a Nash equilibrium strategy. The more efficient social distancing, the less individuals invest prior to vaccine introduction. The blue lines (
) depend on the delay between the start of social-distancing practices and the date when mass-vaccination becomes universally available if individuals use a Nash equilibrium strategy. The more efficient social distancing, the less individuals invest prior to vaccine introduction. The blue lines ( ) do not use social distancing, as the efficiency is below the threshold. The dotted lines represent the minimal asymptotic epidemic costs necessary to stop an epidemic.
) do not use social distancing, as the efficiency is below the threshold. The dotted lines represent the minimal asymptotic epidemic costs necessary to stop an epidemic.References
-
- Dawood F, Jain S, Finelli L, Shaw M, Lindstrom S, et al. Emergence of a novel swine-origin influenza A (H1N1) virus in humans. New England Journal of Medicine. 2009;360:2605–15. - PubMed
-
- Del Valle S, Hethcote H, Hyman JM, Castillo-Chavez C. Effects of behavioural changes in a smallpox attack model. Mathematical Biosciences. 2005;195:228–251. - PubMed
-
- Hyman JM, Li J. Infection-age structured epidemic models with behavior change or treatment. Journal of Biological Dynamics. 2007;1:109–131. - PubMed
-
- Reluga TC, Medlock J. Resistance mechanisms matter in SIRS models. Mathematical Biosciences and Engineering. 2007;4:553–563. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

