Phylogenetic tree reconstruction accuracy and model fit when proportions of variable sites change across the tree

Abstract

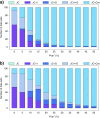
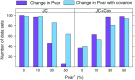
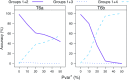
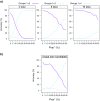
Commonly used phylogenetic models assume a homogeneous process through time in all parts of the tree. However, it is known that these models can be too simplistic as they do not account for nonhomogeneous lineage-specific properties. In particular, it is now widely recognized that as constraints on sequences evolve, the proportion and positions of variable sites can vary between lineages causing heterotachy. The extent to which this model misspecification affects tree reconstruction is still unknown. Here, we evaluate the effect of changes in the proportions and positions of variable sites on model fit and tree estimation. We consider 5 current models of nucleotide sequence evolution in a Bayesian Markov chain Monte Carlo framework as well as maximum parsimony (MP). We show that for a tree with 4 lineages where 2 nonsister taxa undergo a change in the proportion of variable sites tree reconstruction under the best-fitting model, which is chosen using a relative test, often results in the wrong tree. In this case, we found that an absolute test of model fit is a better predictor of tree estimation accuracy. We also found further evidence that MP is not immune to heterotachy. In addition, we show that increased sampling of taxa that have undergone a change in proportion and positions of variable sites is critical for accurate tree reconstruction.

FIGURE 1.

Simulations were done on a 4-taxon tree: T₄=((A,H),(I,P)) (solid lines), two 6-taxon trees: $T_{6a}=($(A,(E,H)),((I,L),P)) (solid and light dashed lines) and $T_{6b}=($((A,D),H),(I,(M,P))) (solid and dark dashed lines), an 8-taxon tree: $T_8=\left(\right($(A,D),(E,H)),((I,L),(M,P))) solid and both light and dark dashed lines, and a 16-taxon tree: T₁₆=((((A,B),(C,D)),((E,F),(G,H))),(((I,J),(K,L)),((M,N),(O,P)))) (all lines). At the root, 80% of the sites were set as invariable. Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50) percent of the invariable sites were reset to be variable in 2 events marked as “1st_event” and “2nd_event.”

FIGURE 2.

A description of the variable and invariable sites in the simulated data. When sequences are simulated without the covarion model, the number of variable sites is equal to the proportion of variable sites (Pvar) multiplied by the number of sites and thus the number of invariable sites is equal to the proportion of invariable sites (Pinv) multiplied by the number of sites. However, when sequences are simulated with the covarion model, the number of variable sites is equal to the proportion of variable sites (Pvar) multiplied by the proportion of sites that are “on” (i.e., variable) under the covarion model (Cov “on”) and the number of sites; the number of invariable sites is then equal to the proportion of invariable sites (Pinv) multiplied by the number of sites plus the proportion of variable sites (Pvar) multiplied by the proportion of sites that are “off” (i.e., invariable) under the covarion model (Cov “off”) and the number of sites. A site can therefore be invariable at a certain time if a) it is part of Pinv or b) it is part of Cov “off.”

FIGURE 3.

Tree reconstruction accuracy for the 4-taxon simulations without the covarion model. Bayesian analysis was done using JC, JC with invariable sites (JC + I), JC with a gamma distribution (JC + G), JC with invariable sites and a gamma distribution (JC + I + G), and JC with the covarion model (JC + Cov). For each model, the sum of the proportional frequencies of each of the 3 possible splits of the groups (1 + 2 vs. 3 + 4, 1 + 3 vs. 2 + 4, and 1 + 4 vs. 2 + 3) is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50) percent of the invariable sites that were reset to be variable in the 2 events.

FIGURE 4.

Tree reconstruction accuracy for the 4-taxon simulations with the covarion model. Bayesian analysis was done using JC, JC + I, JC + G, JC + I + G, and JC + Cov. For each model, the sum of the proportional frequencies of each of the 3 possible splits of the groups (1 + 2 vs. 3 + 4, 1 + 3 vs. 2 + 4, and 1 + 4 vs. 2 + 3) is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50).

FIGURE 5.

Best-fit model for the 4-taxon simulations a) without and b) with the covarion model. Comparison of the number of times each of the 5 models (JC, JC + I, JC + G, JC + I + G, and JC + Cov) was found to be the best-fit model using the a direct comparison of the harmonic means of the estimated marginal likelihoods.

FIGURE 6.

Absolute model-adequacy assessment for data simulated with and without the covarion model for an increasing Pvar⁺=(0, 10, 30, 50). The number of times each model (JC and JC + Cov) was rejected at the 1% level is shown. The JC + I, JC + G, and JC + I + G models were never rejected.

FIGURE 7.

The effect of taxon sampling on reconstruction accuracy of the main split of the tree T (Groups 1 + 2 vs. Groups 3 + 4). The reconstruction accuracy for the 4-, 8-, and 16-taxon simulations using the JC + Cov model is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30).

FIGURE 8.

Comparison of reconstruction accuracy of the main split of the tree T (Groups 1 + 2 vs. Groups 3 + 4) for general increased taxon sampling versus increased taxon sampling under the 2 events. The tree reconstruction accuracy for the data simulated under $T_{6a}=($(A,(E,H)),((I,L),P)) and $T_{6b}=($((A,D),H),(I,(M,P))) using the JC + Cov model is shown for an increasing Pvar⁺=(0, 10, 20, 30, 40, 50).

FIGURE 9.

Tree reconstruction accuracy using MP. a) The effect of taxon sampling on reconstruction accuracy of the main split of the tree T (Groups 1 + 2 vs. Groups 3 + 4). b) Tree estimation for the 4-taxon simulations with uncorrelated events (the positions of sites that switch state are independent). The tree reconstruction accuracy is shown for an increasing Pvar⁺=(0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50).