Sub-AQUA: real-value quality assessment of protein structure models

Abstract

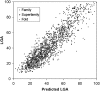
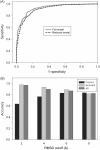
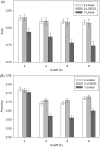
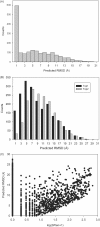
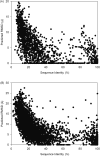
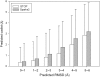
Computational protein tertiary structure prediction has made significant progress over the past years. However, most of the existing structure prediction methods are not equipped with functionality to predict accuracy of constructed models. Knowing the accuracy of a structure model is crucial for its practical use since the accuracy determines potential applications of the model. Here we have developed quality assessment methods, which predict real value of the global and local quality of protein structure models. The global quality of a model is defined as the root mean square deviation (RMSD) and the LGA score to its native structure. The local quality is defined as the distance between the corresponding Calpha positions of a model and its native structure when they are superimposed. Three regression methods are employed to combine different types of quality assessment measures of models, including alignment-level scores, residue-position level scores, atomic-detailed structure level scores and composite scores. The regression models were tested on a large benchmark data set of template-based protein structure models of various qualities. In predicting RMSD and the LGA score, a combination of two terms, length-normalized SPAD, a score that assesses alignment stability by considering suboptimal alignments, and Verify3D normalized by the square of the model length shows a significant performance, achieving 97.1 and 83.6% accuracy in identifying models with an RMSD of <2 and 6 A, respectively. For predicting the local quality of models, we find that a two-step approach, in which the global RMSD predicted in the first step is further combined with the other terms, can dramatically increase the accuracy. Finally, the developed regression equations are applied to assess the quality of structure models of whole E. coli proteome.

Fig. 1

Actual RMSD of structure models relative to predicted RMSD. RMSD is predicted by regression models using log(SPAD) and log(Verify3D/L²) as predictor variables. Regression models are built on all the structural models in the L–E set. The linear regression model (Eqn. 3) is used.

Fig. 2

Predicted and actual LGA score. LGA is predicted by a linear regression model using log(SPAD), seqID and Verify3D/L² as predictor variables (Eqn. 4). Regression model is built on all the structural models in the L–E data set. Correlation coefficient between true LGA and predicted LGA is 0.88.

Fig. 3

Discriminating correct structure models from incorrect models by logistic regression. (A) ROC curve of a logistic regression with all the twenty variables (the full model) and one with log(SPAD) and log(Verify3D/L²) (the reduced model). Correct models are those which have an RMSD of 6 Å or lower to native. (B) Predicting correct/incorrect models by the reduced logistic regression model. Correct models are defined as those with an RMSD of 2, 4, 6 and 8 Å or lower.

Fig. 4

Classification of structure models into four different categories. A multinomial logistic regression model is constructed to classify structure models into four different RMSD ranges, less than 3, 3–6, 6–9 or larger than 9 Å. x-axis represents the true classification of the models in terms of the four categories. y-axis shows the proportions of the models that are predicted to be the four different categories. The percentage of the correctly classified structure models to each RMSD range is as follows. The numbers are ordered for <3, 3–6, 6–9, >9 Å: The family level data set: 53.8, 69.2, 32.7, 56.1%. The superfamily level: 0, 61.2, 45.7, 85.6%. The fold level (there was no model with RMSD <3 Å), 8.6, 36.2, 92.4%. All data set: 47.5, 60.4, 39.2, 82.4%.

Fig. 5

Comparison of hierarchical regression approaches and regular linear regression in terms of predicting Cα distance of residues in structural models. 2_Linear and 2_LOESS are the hierarchical approaches, in which the global RMSD is predicted first and then used in the second step as one of the independent variables. 2_Linear uses linear regression while 2_LOESS uses LOESS regression. Residues in structure models are classified into correct or incorrect, using threshold values of Cα distance of 2, 4, 6 and 8 Å. The cross-validation using four subsets of data for training and one for testing is performed fifty times and the average and the standard deviation are shown. The total number of residues is 159,947 in 5232 structure models. The proportion of correct positioned residues with the cutoff of 2, 4, 6 and 8 Å is 27.2, 48.1, 59.4 and 66.6%, respectively. (A) AUC of the three models with different RMSD cutoffs. (B) Accuracy of the three models with different RMSD cutoffs.

Fig. 6

Correlation between the predicted RMSD by Sub-AQUA and the true RMSD of CASP7 models. The linear regression is used. Models are divided into four categories (HA-TBM, TBM, TBM-FM and FM) according to the CASP7 criteria. The correlation coefficients of the predicted and actual RMSD are 0.536, 0.419, 0.350 and 0.438 for the HA-TBM, TBM, TBM-FM and FM category, respectively. These correlation coefficients are computed using all the structure models from all the targets in the category together.

Fig. 7

Average RMSD of the top models. Different MQAP scores are used to rank all available models for each target protein in CASP7 and the top 1-ranked model is selected. The average RMSD is calculated over all the top 1 models selected by each MQAP score. Models are divided into four categories (HA-TBM, TBM, TBM-FM and FM) according to the CASP7 criteria and ‘All’ denotes all the models pooled together. The MQAPs is ordered by the average RMSD for the All category.

Fig. 8

Distribution of the predicted RMSD of E.coli protein models. RMSD is predicted using the linear regression using log(SPAD) and log(Verify3D/L²) as predictor variables. (A) the GTOP-Nest set and (B) the SPARKS2 set.

Fig. 9

Predicted RMSD relative to the sequence length of structure models. (A) The GTOP-Nest structural models. (B) the SPARKS2 set.

Fig. 10

Predicted RMSD of the structural models is plotted against the sequence identity between the target protein and its template. (A) The GTOP-Nest structural models. (B) The SPARKS2 set.

Fig. 11

The range of predicted Cα distance relative to predicted global RMSD. The standard deviation is shown by the error bars. White bars, the GTOP-Nest structural models; gray bars, the SPARKS2 set.

Fig. 12

Examples of estimated local structure quality (the Cα distance) of E. coli proteins. The Cα distance is represented in the ‘sausage representation’, where the radius of the tube is proportional to the estimated Cα distance. The Cα distance is predicted by the two-layer linear regression model (Fig. 4). (A), (C) and (E) are predicted by the GTOP-Nest procedure and (B), (D) and (F) are predicted by the SPARKS2 procedure. Associated graphs show predicted Cα distance. Black/gray boxes in the graph show location of α helices/β strands in the chain. (A), yccK (predicted sulfite reductase subunit), the template structure used is 1sauA. The sequence identity (seqID) between the gene and the template is 38%. The global RMSD is predicted 0.7 Å. (B), rpsK (30S ribosomal subunit protein S11), template: 1s1hK, seqID: 35%. Predicted global RMSD: 0.6 Å. (C), yiqP (function unknown), template: 1iktA, seqID: 15%, predicted RMSD: 3.1 Å. (D), holD (DNA polymerasae psi subunit), template: 1em8B, seqID: 80%, predicted RMSD: 3.14 Å. (E), yfgD (predicted oxidoreductase), template: 1rw1A, seqID: 15%, predicted RMSD: 5.3 Å. (F), rhaR (positive regulatory gene), template: 1ft9A, seqID: 7%, predicted RMSD: 5.3 Å.