Reactive control and its operation limits in responding to a novel slip in gait

Abstract

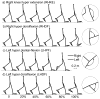
The purposes of this study were: (1) to examine the reactive control of the resultant joint moments at the lower limbs in response to a novel and unannounced slip; (2) to establish individualized forward-dynamics models; and (3) to explore personal potential by determining the operation limits of these moments at each lower limb joint, beyond which the resulting motion at this or other joints will exceed its/their normal range(s). Ten young subjects' kinematics and kinetics, collected during regular walking and during their first exposure to a novel and unannounced slip, were randomly selected from an existing database. An inverse-dynamics approach was applied to derive their (original) resultant joint moments, which were then used as input to establish forward-dynamics models, each including an individualized 16-element foot model to simulate ground reaction force. A simulated annealing (SA) algorithm was applied to modify the original moments, so that the subsequent output (baseline) moments can closely reproduce these subjects' recorded motion. A systematic alteration of the baseline moments was employed to determine the operation limits. The results revealed that the subjects reactively increased the hip extensor and knee flexor moments and reduced their ankle plantar flexor moments of their single-stance limb following slip onset. The "baseline" correction of the original moments can reach as much as 21% of the original moments. The analysis of the operation limits revealed that these individuals may be able to further increase their knee flexors more so than increase the hip extensors or reduce ankle plantar flexors before causing abnormal joint movement. Such systematic approach opens the possibility to properly assess an individual's rehabilitation potential, and to identify whether this person's strength is the limiting factor for stability training.

Fig. 1

Schematic of the 7-link, 9-degree-of-freedom, sagittal-plane model of the human body. The vector q= [x,y,θ_1,θ₂,···θ₇] represents the generalized coordinates of the model. Coordinates x, y, and θ₁ specify the position and orientation of the right (stance or slipping) foot, which is the base segment of the model following the left (swing or recovery) foot liftoff after slip onset, with reference to the inertial reference frame (X, Y, Z). Joint angles θ_i (i = 2,3,4,···,7) correspondingly specify the angles of the ankle, knee, hip of the stance limb (solid line) and the hip, knee, and ankle of the swing limb (dashed line). The positive X-axis is in the direction of forward progression, and the positive Y-axis is upward. Positive joint rotation is along the positive Z-axis (counterclockwise) for the stance limb (solid line), and its sign is reversed (clockwise) for the swing limb (dashed line).

Fig. 2

Schematic of the procedure to derive joint moments which can reproduce the experimentally measured kinematics (the joint angles and base of support displacement) and kinetics (the ground reaction forces) during a slip in gait. These derived joint moments are called baseline moments. The procedure, including two main parts: forward-dynamics simulation and optimization, was used to modify the original moments which were derived by traditional inverse-dynamics approach from experimental measurements to baseline moments. A simulated annealing (SA) algorithm was used to perform the optimization routine. The iteration process is indicated by the narrow arrow.

Fig. 3

The profile (mean ± SD) of lower limb joint moments across 10 subjects, calculated from an inverse-dynamics (original moments, solid line) and from our forward-dynamics approach (baseline moments, dashed line), during single-stance phase (single-limb support of the right foot) from left foot liftoff (LLO) to its touchdown (LTD) for right (stance) (a) hip, (b) knee, and (c) ankle. The instant of LLO typically occurs ~160 ms after slip onset (OS). Also shown are the average joint moments during the single-stance phase of the regular walking trial, across the same subject group (dash-dotted line). The arrows indicate the changes from these moments measured in regular gait, that are reflective of the reactive control at each joint, which these subjects actually had executed in response to a novel and unannounced slip in gait. It is obvious that this response includes increasing hip extensor and knee flexor and reducing ankle plantar-flexor moments during the slip trials. The joint moments are normalized to body mass.

Fig. 4

A representative simulation sample of single-stance phase, from left (swing) foot liftoff (LLO) to its touchdown (LTD), for a subject (body mass = 72.6 kg, body height = 1.70 m). The instant of LLO typically occurs ~160 ms after slip onset (OS). This shows that the optimization-derived (corrected) results (in dashed line) closely tracked the experimental (original in solid line) kinematics and kinetics, by our optimization/forward-dynamics simulation procedure. In comparison, the uncorrected kinematics (in dash-dotted line) was computed by forward-dynamics approach without using optimization algorithm to reduce error, which is clearly visible. The kinematics (angular or linear displacement) & the joint moments of the (a & b) hip, (c & d) knee, (e & f) ankle, (g & h) foot, and the horizontal & vertical component of the ground reaction force (GRF) (i & j) are all demonstrated at the right limb. The joint moments are normalized to body mass and the GRF is normalized to body weight, bw.

Fig. 5

The group mean (n = 10) of the operation limits for the resultant joint moments of stance (a) hip, (b) knee, and (c) ankle during the entire single-stance phase from left (swing) foot liftoff (LLO) to its touchdown (LTD). During an altered simulation, the joint moments are altered by adding or subtracting a fixed interval Δτ at 10⁻³ Nm/kg. Also shown are the average baseline moments for each stance side joint across all subjects. For each joint, the greater operation limit is demonstrated. The upper and lower bounds of the operation limits are defined as the maximum allowed alteration size imparted to the baseline moments before the joint angles at any instant of the entire single-stance phase begin to exceed 1 SD above the standard range of motion for that particular joint, or their moments exceed the limits of the corresponding muscle strength illustrated by the thin horizontal lines and the values normalized by body mass, i.e., in Nm/kg^,.

Fig. 6

Four types of failure encountered in altered simulation: (a) hyper extension at right (stance) knee (RHKE), (b) hyper dorsiflexion at right ankle (RHDF), (c) hyper plantar-flexion at left ankle (LHPF), and (d) hyper dorsiflexion at left ankle (LHDF). See Table 2 for detailed definition of failure type. The numbers beneath the stick figures indicate the simulation time in percentage, and the asterisk represents the COM position. The triangle is the starting position of the right heel at left foot liftoff. The altered simulation would fail once the perturbed joint angles deviated by 1 SD from the corresponding joint’s range of motion. A small circle on the stick figures was used to identify the joint which encountered the unrealistic movement. To illustrate the joint movement clearly, the small circles were enlarged.

Fig. 7

Comparison of the group mean of lower limb joint moments at stance side between our study and those reported by other researchers^,. All three sets of joint moments were derived by an inverse-dynamics approach during the single-stance phase from left (swing) liftoff (LLO) to its touchdown (LTD) in gait-slip. Joint moments are normalized to body mass in Nm/kg.