Inferring combinatorial association logic networks in multimodal genome-wide screens

Abstract

Motivation: We propose an efficient method to infer combinatorial association logic networks from multiple genome-wide measurements from the same sample. We demonstrate our method on a genetical genomics dataset, in which we search for Boolean combinations of multiple genetic loci that associate with transcript levels.

Results: Our method provably finds the global solution and is very efficient with runtimes of up to four orders of magnitude faster than the exhaustive search. This enables permutation procedures for determining accurate false positive rates and allows selection of the most parsimonious model. When applied to transcript levels measured in myeloid cells from 24 genotyped recombinant inbred mouse strains, we discovered that nine gene clusters are putatively modulated by a logical combination of trait loci rather than a single locus. A literature survey supports and further elucidates one of these findings. Due to our approach, optimal solutions for multi-locus logic models and accurate estimates of the associated false discovery rates become feasible. Our algorithm, therefore, offers a valuable alternative to approaches employing complex, albeit suboptimal optimization strategies to identify complex models.

Availability: The MATLAB code of the prototype implementation is available on: http://bioinformatics.tudelft.nl/ or http://bioinformatics.nki.nl/.

Fig. 1.

Schematic overview of data and association inference. (A) A panel of BXD mice that is densely genotyped and expression profiled. The genotype data can be considered as binary vectors by choosing a binary encoding of the alleles (in the figure D = true and B = false) and putting thresholds that divide the genome into loci such that each locus differs in at least one element from its neighbors. The cartoon shows that good association is obtained between Locus 5 and Gene 7 because elevated expression is consistently observed in conjunction with the D allele of Locus 5. (B) Interaction among genetic features may destroy direct associations between individual loci and genes. The cartoon shows that configurations exist in which the gene expression can only be predicted by considering two loci simultaneously (using Boolean xor logic). (C) By inferring CAL networks, interaction among genetic features is taken into account in the association inference. Inferring CAL networks is achieved by selecting the input loci with the selection function 𝒮 and combining these with the appropriate Boolean function ℬ, such that the association (as measured by a scoring function f) between the network output and the gene of interest is maximized.

Fig. 2.

Association versus approximated association. (A) Example gene expression vector (circles) split in x₀ and x₁ according to y_opt. The magenta line denotes the association measure f, defined in Equation (2), as a function of a threshold t that splits the expression vector in x₀ and x₁. The blue triangles indicate the error weights w(τ) that result after optimizing them. 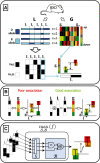(B and C) 500 random samples that are generated by introducing up to seven bit-flips in y^opt to show the relation between and f. The red dot indicates and f values for y^opt. (B) shows the samples in case the weights are assumed equal. Although the trend of the data is monotonically increasing, a large spread around this trend is observed. (C) shows the same samples in case the weights are optimized, resulting in a near one-to-one relation between and f.

Fig. 3.

Computation of solution sets for each sample. (A) Example data from Figure 1A. (B) The topology and the truth table of the Boolean function ℬ under investigation. (C) Explanation by example of the calculation of V^(τ), the set of all possible input combinations to ℬ such that y^opt(τ) = y(τ). This panel shows how V⁽¹⁾ is determined. Since y^opt(1) = 1, the rows from the truth table for which y = 1 are applicable, i.e, r = {2, 4, 6, 7}. According to r = 2, the desired output for τ = 1 is obtained by selecting any of the loci that are ‘0’ for inputs i₁ and i₂, and loci that are ‘1’ for input i₃. Accordingly, for i₁ we may select from the set: {l₁, l₂, l₄}. This can be efficiently calculated by taking the xnor (evaluates to ‘1’ when both inputs are equal) between row τ = 1 from the data matrix and the row r = 2 from the truth table, as shown in (C). Observe that the result is an efficient encoding of all the possible input combinations that satisfy y^opt(1) while using r = 2 from the truth table. In general, we denote this set by V_r^(τ), and its binary encoding by . To determine the complete set of valid input combinations for τ = 1, rows 4, 6 and 7 need to be considered in a similar fashion. V⁽¹⁾ is now determined by taking the union of the subsets, i.e. V⁽¹⁾ = V₂⁽¹⁾∪V₄⁽¹⁾∪V₆⁽¹⁾∪V₇⁽¹⁾, which, in binary form, may be represented by a concatenation of , , and . (D) This panel shows the valid input combinations for τ = 1 and τ = 3 in binary representation (i.e. and ). For any set of samples C the input combinations for which the output equals y^opt can be obtained by taking the intersection of the individual sets. In binary representation, this is equivalent to taking the row-wise cartesian product (row-wise product of all combinations of rows), as is shown in the panel.

Fig. 4.

Algorithm performance in terms of accuracy and runtime under various conditions. (A) Bargraph displaying accuracy for different network topologies and different values of the f-score. For each of the network topologies the 75th percentile of the solution distribution is also given, showing that for solutions in the tail 100% accuracy is obtained. For the two missing bars in the 4-6 and 5-6 bins no solutions were found. (B) and C) Runtimes for different network topologies and dataset sizes. The horizontal lines reflect runtimes for exhaustive search. From bottom to top these represent the runtimes for: a single input network, two input network and three input network with one, two and four times the number of predictors, respectively.

Fig. 5.

(A) Bargraph with an overview of the number of gene clusters for which a significant (10% FDR) solution is found. Network topologies are sorted according to the 10% FDR level (blue line). (B) CAL networks significant at 10% FDR. The color and shape of the symbols correspond to the symbols used in (C). Small circles at the inputs of the networks denote negation, i.e. for these inputs the mapping from allele to binary representation is switched. We also indicate whether the best single marker coincides, for that gene cluster, with one of the inputs of the CAL network. (C) Marker/probe-plot for the top CAL networks showing both the eQTLs (blue crosses) and ceQTLs (sets of colored symbols of various shapes). The colors and shapes of the markers refer to the network topologies listed in (B). Horizontal gray lines connect the inputs and the output of the CAL network. Because probes were clustered, it occurs that the ceQTLs map to multiple probes in case these probes were part of the same cluster. The numeric labels near the the colored symbols correspond to the input of the network. Notably, some probes seem to be predicted by more ceQTLs than there are inputs to the CAL network reported. This occurs when there are multiple combinations of markers that show the same association with the gene expression level of the network output, and can be explained by similarity among markers. The cis-band (diagonal) is clearly visible, and in one occasion contains a ceQTL. Overlap among ceQTLs from different networks is marked by red dashed lines, overlap between ceQTLs and eQTLs by black dashed lines.

Fig. 6.

Input regions of the CAL network for Lilrb4 The line graphs give the f-score for association between the output gene and the individual markers (blue) and the network output (red). The latter was computed by taking the maximum f-score of the network using the marker under evaluation for one input and any of the other markers for the second input of the network. Where possible the IDs of the genetic markers are given, but some were omitted for readability. The dot plots gives the expression values separated by network output (right) and the best markers in the inputs (left). Finally, for one particular combination of markers the genotype for all strains is depicted as a Boolean heat map. In these diagrams, the not gates were already incorporated.