Assessing the functional coherence of gene sets with metrics based on the Gene Ontology graph
- PMID: 20529941
- PMCID: PMC2881388
- DOI: 10.1093/bioinformatics/btq203
Assessing the functional coherence of gene sets with metrics based on the Gene Ontology graph
Abstract
Motivation: The results of initial analyses for many high-throughput technologies commonly take the form of gene or protein sets, and one of the ensuing tasks is to evaluate the functional coherence of these sets. The study of gene set function most commonly makes use of controlled vocabulary in the form of ontology annotations. For a given gene set, the statistical significance of observing these annotations or 'enrichment' may be tested using a number of methods. Instead of testing for significance of individual terms, this study is concerned with the task of assessing the global functional coherence of gene sets, for which novel metrics and statistical methods have been devised.
Results: The metrics of this study are based on the topological properties of graphs comprised of genes and their Gene Ontology annotations. A novel aspect of these methods is that both the enrichment of annotations and the relationships among annotations are considered when determining the significance of functional coherence. We applied our methods to perform analyses on an existing database and on microarray experimental results. Here, we demonstrated that our approach is highly discriminative in terms of differentiating coherent gene sets from random ones and that it provides biologically sensible evaluations in microarray analysis. We further used examples to show the utility of graph visualization as a tool for studying the functional coherence of gene sets.
Availability: The implementation is provided as a freely accessible web application at: http://projects.dbbe.musc.edu/gosteiner. Additionally, the source code written in the Python programming language, is available under the General Public License of the Free Software Foundation.
Supplementary information: Supplementary data are available at Bioinformatics online.
Figures


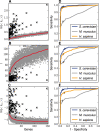
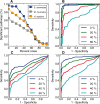

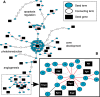
Similar articles
-
Revealing functionally coherent subsets using a spectral clustering and an information integration approach.BMC Syst Biol. 2012;6 Suppl 3(Suppl 3):S7. doi: 10.1186/1752-0509-6-S3-S7. Epub 2012 Dec 17. BMC Syst Biol. 2012. PMID: 23282411 Free PMC article.
-
GRYFUN: a web application for GO term annotation visualization and analysis in protein sets.PLoS One. 2015 Mar 20;10(3):e0119631. doi: 10.1371/journal.pone.0119631. eCollection 2015. PLoS One. 2015. PMID: 25794277 Free PMC article.
-
GS2: an efficiently computable measure of GO-based similarity of gene sets.Bioinformatics. 2009 May 1;25(9):1178-84. doi: 10.1093/bioinformatics/btp128. Epub 2009 Mar 16. Bioinformatics. 2009. PMID: 19289444 Free PMC article.
-
Beyond standard pipeline and p < 0.05 in pathway enrichment analyses.Comput Biol Chem. 2021 Jun;92:107455. doi: 10.1016/j.compbiolchem.2021.107455. Epub 2021 Feb 12. Comput Biol Chem. 2021. PMID: 33774420 Free PMC article. Review.
-
Gene set enrichment analysis: performance evaluation and usage guidelines.Brief Bioinform. 2012 May;13(3):281-91. doi: 10.1093/bib/bbr049. Epub 2011 Sep 7. Brief Bioinform. 2012. PMID: 21900207 Free PMC article. Review.
Cited by
-
The Growing Importance of CNVs: New Insights for Detection and Clinical Interpretation.Front Genet. 2013 May 30;4:92. doi: 10.3389/fgene.2013.00092. eCollection 2013. Front Genet. 2013. PMID: 23750167 Free PMC article.
-
Identifying informative subsets of the Gene Ontology with information bottleneck methods.Bioinformatics. 2010 Oct 1;26(19):2445-51. doi: 10.1093/bioinformatics/btq449. Epub 2010 Aug 11. Bioinformatics. 2010. PMID: 20702400 Free PMC article.
-
GO-based functional dissimilarity of gene sets.BMC Bioinformatics. 2011 Sep 1;12:360. doi: 10.1186/1471-2105-12-360. BMC Bioinformatics. 2011. PMID: 21884611 Free PMC article.
-
From data towards knowledge: revealing the architecture of signaling systems by unifying knowledge mining and data mining of systematic perturbation data.PLoS One. 2013 Apr 23;8(4):e61134. doi: 10.1371/journal.pone.0061134. Print 2013. PLoS One. 2013. PMID: 23637789 Free PMC article.
-
Graphical algorithm for integration of genetic and biological data: proof of principle using psoriasis as a model.Bioinformatics. 2015 Apr 15;31(8):1243-9. doi: 10.1093/bioinformatics/btu799. Epub 2014 Dec 4. Bioinformatics. 2015. PMID: 25480373 Free PMC article.
References
-
- Alexa A, et al. Improved scoring of functional groups from gene expression data by decorrelating GO graph structure. Bioinformatics. 2006;22:1600–1607. - PubMed
-
- Barabási A, Oltvai Z. Network biology: understanding the cell's functional organization. Nat. Rev. Genet. 2004;5:101–114. - PubMed
-
- Cho R, et al. Transcriptional regulation and function during the human cell cycle. Nat. Genet. 2001;27:48–54. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

