Optimal workloop energetics of muscle-actuated systems: an impedance matching view
- PMID: 20532203
- PMCID: PMC2880559
- DOI: 10.1371/journal.pcbi.1000795
Optimal workloop energetics of muscle-actuated systems: an impedance matching view
Abstract
Integrative approaches to studying the coupled dynamics of skeletal muscles with their loads while under neural control have focused largely on questions pertaining to the postural and dynamical stability of animals and humans. Prior studies have focused on how the central nervous system actively modulates muscle mechanical impedance to generate and stabilize motion and posture. However, the question of whether muscle impedance properties can be neurally modulated to create favorable mechanical energetics, particularly in the context of periodic tasks, remains open. Through muscle stiffness tuning, we hypothesize that a pair of antagonist muscles acting against a common load may produce significantly more power synergistically than individually when impedance matching conditions are met between muscle and load. Since neurally modulated muscle stiffness contributes to the coupled muscle-load stiffness, we further anticipate that power-optimal oscillation frequencies will occur at frequencies greater than the natural frequency of the load. These hypotheses were evaluated computationally by applying optimal control methods to a bilinear muscle model, and also evaluated through in vitro measurements on frog Plantaris longus muscles acting individually and in pairs upon a mass-spring-damper load. We find a 7-fold increase in mechanical power when antagonist muscles act synergistically compared to individually at a frequency higher than the load natural frequency. These observed behaviors are interpreted in the context of resonance tuning and the engineering notion of impedance matching. These findings suggest that the central nervous system can adopt strategies to harness inherent muscle impedance in relation to external loads to attain favorable mechanical energetics.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures
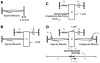
 , stiffness
, stiffness  and damping constant
and damping constant  ). (C) An idealized, impedance-free force source acting on the same load. The force source is limited in absolute magnitude by
). (C) An idealized, impedance-free force source acting on the same load. The force source is limited in absolute magnitude by  . (D) Antagonist muscles acting against a common admitting load. In this setup, muscles communicate with each other mechanically through the common load. The impedance of one muscle forms part of the load of the other. Note that in (A) the motion is imposed on the muscle irrespective of its contractile force, while in (B), (C) and (D) cyclic motions result from applied muscle or actuator forces. The coordinates and definitions of the variables used for system modeling are shown in panel (D). The contractile forces are
. (D) Antagonist muscles acting against a common admitting load. In this setup, muscles communicate with each other mechanically through the common load. The impedance of one muscle forms part of the load of the other. Note that in (A) the motion is imposed on the muscle irrespective of its contractile force, while in (B), (C) and (D) cyclic motions result from applied muscle or actuator forces. The coordinates and definitions of the variables used for system modeling are shown in panel (D). The contractile forces are  and
and  for the agonist and antagonist muscles respectively, whereas the net force is
for the agonist and antagonist muscles respectively, whereas the net force is  . The lengths of the muscles is
. The lengths of the muscles is  and
and  , and the variables
, and the variables  and
and  are in the load reference frame. The electrical stimulus delivered to the muscles comprises the system input, and is indicated by
are in the load reference frame. The electrical stimulus delivered to the muscles comprises the system input, and is indicated by  and
and  .
.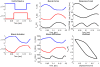
 seconds, corresponding to an oscillation frequency of 5 Hz. Plots show the bang-bang control inputs [dimensionless] and corresponding activation [dimensionless], muscle forces [N], time-varying stiffnesses [N/m], the motion of the mass-spring-damper system (displacement, velocity, and the net power imparted per kg of muscle), and the resulting workloop. In the plots, blue traces pertain to the agonist muscle, the red traces to the antagonist muscle, and black traces refer to the net effects of both muscles and the load. Note that this particular solution exhibits co-activation as evidenced by the degree of overlap in the activation signals, and also in the control signals. This co-activation was required to stiffen the overall system to accommodate the relatively high-frequency of excitation required.
seconds, corresponding to an oscillation frequency of 5 Hz. Plots show the bang-bang control inputs [dimensionless] and corresponding activation [dimensionless], muscle forces [N], time-varying stiffnesses [N/m], the motion of the mass-spring-damper system (displacement, velocity, and the net power imparted per kg of muscle), and the resulting workloop. In the plots, blue traces pertain to the agonist muscle, the red traces to the antagonist muscle, and black traces refer to the net effects of both muscles and the load. Note that this particular solution exhibits co-activation as evidenced by the degree of overlap in the activation signals, and also in the control signals. This co-activation was required to stiffen the overall system to accommodate the relatively high-frequency of excitation required.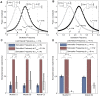
 Hz,
Hz,  and
and  N/m (A), and
N/m (A), and  Hz,
Hz,  and
and  N/m (B). (C & D) Experimental measurements of power ratios shown for each measurement set. Workloop power measurements in each set are normalized by
N/m (B). (C & D) Experimental measurements of power ratios shown for each measurement set. Workloop power measurements in each set are normalized by  . The error bars at
. The error bars at  are therefore equal to zero by definition. Both figures show that
are therefore equal to zero by definition. Both figures show that  and
and  . The asterisks indicated the
. The asterisks indicated the  value, with (**) for
value, with (**) for  and (*) for
and (*) for  . (C) Measurements taken across 3 muscle for load natural frequency
. (C) Measurements taken across 3 muscle for load natural frequency  Hz,
Hz,  and
and  N/m. (D) Measurements taken across 2 muscles for load natural frequency
N/m. (D) Measurements taken across 2 muscles for load natural frequency  Hz,
Hz,  and
and  N/m.
N/m.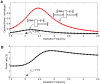
 , which at certain frequencies is substantially higher than 2.
, which at certain frequencies is substantially higher than 2.  is the resonance frequency of the mass-spring-damper unloaded by the muscles. Results shown for
is the resonance frequency of the mass-spring-damper unloaded by the muscles. Results shown for  Hz,
Hz,  and
and  N/m.
N/m.
 (representing mean and standard deviation of the averages of 4 muscle pairs). (A) Workloops of agonist muscle acting individually. (B) Workloops of antagonist muscle acting individually. (C) Workloops of muscle pair stimulated out of phase, producing more work on the same load. Asterisks indicate stimulation points (red is for agonist, blue is for antagonist). The first workloop is atypical as the system converges to a steady-state response and is discarded from energetic computations. All workloops have a counter clock-wise direction, indicating positive muscle work, which equals the energy dissipated in the damper. For all cases the natural frequency of the load was
(representing mean and standard deviation of the averages of 4 muscle pairs). (A) Workloops of agonist muscle acting individually. (B) Workloops of antagonist muscle acting individually. (C) Workloops of muscle pair stimulated out of phase, producing more work on the same load. Asterisks indicate stimulation points (red is for agonist, blue is for antagonist). The first workloop is atypical as the system converges to a steady-state response and is discarded from energetic computations. All workloops have a counter clock-wise direction, indicating positive muscle work, which equals the energy dissipated in the damper. For all cases the natural frequency of the load was  Hz,
Hz,  and
and  N/m. (D) Compiled results for data points similar to A, B and C, with operating frequency = 3 Hz. Data shown across 3 muscle pairs. The workloop energetics of the two muscles working together is not statistically significant from a value of 2 predicted in the theoretical case of linear, impedance-free actuators. (E) Compiled results for data points similar to A, B and C, with operating frequency = 4 Hz. Data shown across 4 muscle pairs. The workloop energetics of the two muscles working together significantly greater than 2. The asterisks indicated the
N/m. (D) Compiled results for data points similar to A, B and C, with operating frequency = 3 Hz. Data shown across 3 muscle pairs. The workloop energetics of the two muscles working together is not statistically significant from a value of 2 predicted in the theoretical case of linear, impedance-free actuators. (E) Compiled results for data points similar to A, B and C, with operating frequency = 4 Hz. Data shown across 4 muscle pairs. The workloop energetics of the two muscles working together significantly greater than 2. The asterisks indicated the  value, with (**) for
value, with (**) for  and (*) for
and (*) for  .
.Similar articles
-
Workloop energetics of antagonist muscles.Conf Proc IEEE Eng Med Biol Soc. 2006;2006:3640-3. doi: 10.1109/IEMBS.2006.260081. Conf Proc IEEE Eng Med Biol Soc. 2006. PMID: 17947046
-
A three filament mechanistic model of musculotendon force and impedance.Elife. 2024 Sep 10;12:RP88344. doi: 10.7554/eLife.88344. Elife. 2024. PMID: 39254193 Free PMC article.
-
An analysis of the sources of musculoskeletal system impedance.J Biomech. 1988;21(12):1011-25. doi: 10.1016/0021-9290(88)90248-5. J Biomech. 1988. PMID: 2577948
-
Biomechanical determinants of pedaling energetics: internal and external work are not independent.Exerc Sport Sci Rev. 2002 Oct;30(4):159-65. doi: 10.1097/00003677-200210000-00004. Exerc Sport Sci Rev. 2002. PMID: 12398112 Review.
-
Insect sound production: transduction mechanisms and impedance matching.Symp Soc Exp Biol. 1995;49:199-218. Symp Soc Exp Biol. 1995. PMID: 8571224 Review.
Cited by
-
Active Viscoelasticity of Sarcomeres.Front Robot AI. 2018 Jun 14;5:69. doi: 10.3389/frobt.2018.00069. eCollection 2018. Front Robot AI. 2018. PMID: 33500948 Free PMC article. Review.
-
Unconstrained muscle-tendon workloops indicate resonance tuning as a mechanism for elastic limb behavior during terrestrial locomotion.Proc Natl Acad Sci U S A. 2015 Oct 27;112(43):E5891-8. doi: 10.1073/pnas.1500702112. Epub 2015 Oct 12. Proc Natl Acad Sci U S A. 2015. PMID: 26460038 Free PMC article.
-
Modeling and simulating the neuromuscular mechanisms regulating ankle and knee joint stiffness during human locomotion.J Neurophysiol. 2015 Oct;114(4):2509-27. doi: 10.1152/jn.00989.2014. Epub 2015 Aug 5. J Neurophysiol. 2015. PMID: 26245321 Free PMC article.
-
Phase shift between joint rotation and actuation reflects dominant forces and predicts muscle activation patterns.PNAS Nexus. 2023 Oct 10;2(10):pgad298. doi: 10.1093/pnasnexus/pgad298. eCollection 2023 Oct. PNAS Nexus. 2023. PMID: 37822766 Free PMC article.
-
Beyond power limits: the kinetic energy capacity of skeletal muscle.J Exp Biol. 2024 Nov 1;227(21):jeb247150. doi: 10.1242/jeb.247150. Epub 2024 Oct 18. J Exp Biol. 2024. PMID: 39234652 Free PMC article. Review.
References
-
- Nishikawa K, Biewener AA, et al. Neuromechanics: an integrative approach for understanding motor control. Integr Comp Biol. 2007;47:16–54. - PubMed
-
- Dickinson MH, Farley CT, Full RJ, Koehl MAR, Kram R, et al. How animals move: An integrative view. Science. 2000;288:100–106. - PubMed
-
- Rolf Pfeifer ML, Iida F. Self-organization, embodiment, and biologically inspired robotics. Science. 2007;318:1088–1093. - PubMed
-
- Hogan N. Adaptive control of mechanical impedance by coactivation of agonist muscles. IEEE Trans Automat Contr. 1984;29:681–690.
-
- Hogan N. The mechanics of multi-joint posture and movement control. Biol Cybern. 1985;52:315–331. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

