W-curve alignments for HIV-1 genomic comparisons
- PMID: 20532248
- PMCID: PMC2879897
- DOI: 10.1371/journal.pone.0010829
W-curve alignments for HIV-1 genomic comparisons
Abstract
Background: The W-curve was originally developed as a graphical visualization technique for viewing DNA and RNA sequences. Its ability to render features of DNA also makes it suitable for computational studies. Its main advantage in this area is utilizing a single-pass algorithm for comparing the sequences. Avoiding recursion during sequence alignments offers advantages for speed and in-process resources. The graphical technique also allows for multiple models of comparison to be used depending on the nucleotide patterns embedded in similar whole genomic sequences. The W-curve approach allows us to compare large numbers of samples quickly.
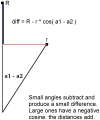
Method: We are currently tuning the algorithm to accommodate quirks specific to HIV-1 genomic sequences so that it can be used to aid in diagnostic and vaccine efforts. Tracking the molecular evolution of the virus has been greatly hampered by gap associated problems predominantly embedded within the envelope gene of the virus. Gaps and hypermutation of the virus slow conventional string based alignments of the whole genome. This paper describes the W-curve algorithm itself, and how we have adapted it for comparison of similar HIV-1 genomes. A treebuilding method is developed with the W-curve that utilizes a novel Cylindrical Coordinate distance method and gap analysis method. HIV-1 C2-V5 env sequence regions from a Mother/Infant cohort study are used in the comparison.
Findings: The output distance matrix and neighbor results produced by the W-curve are functionally equivalent to those from Clustal for C2-V5 sequences in the mother/infant pairs infected with CRF01_AE.
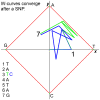
Conclusions: Significant potential exists for utilizing this method in place of conventional string based alignment of HIV-1 genomes, such as Clustal X. With W-curve heuristic alignment, it may be possible to obtain clinically useful results in a short time-short enough to affect clinical choices for acute treatment. A description of the W-curve generation process, including a comparison technique of aligning extremes of the curves to effectively phase-shift them past the HIV-1 gap problem, is presented. Besides yielding similar neighbor-joining phenogram topologies, most Mother and Infant C2-V5 sequences in the cohort pairs geometrically map closest to each other, indicating that W-curve heuristics overcame any gap problem.
Conflict of interest statement
Figures



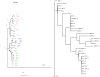
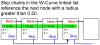
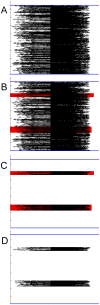
References
-
- Wu D, Roberge J, Cork DJ, Nguyen BG, Grace T. 1993;33:308–315. Computer visualization of long genomic sequences, in Visualization 1993, IEEE Press, New York City, New York, CP.
-
- Almeida JS, Carrico JA, Maretzek A, Noble PA, Fletcher M. Analysis of genomic sequences by chaos game representation. Bioinformatics. 2001;17(5):429–437. - PubMed
-
- Huang G, Liao B, Li Y, Yu Y. Similarity studies of DNA sequences based on a new 2D graphical representation. Biophysical Chem. 2009;143:55–59. - PubMed
-
- Cork DJ, Marland E, Zmuda J, Hutch TB. Valafar F, editor. Achieving Congruency of Phylogenetic Trees Generated by W-curves of Genomic Sequences. 2002. pp. 32–40. Techniques in Bioinformatics and Medical Informatics. Part I. Bioinformatics. Ann. N. Y. Acad. Sci. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

