Probing static disorder in Arrhenius kinetics by single-molecule force spectroscopy
- PMID: 20534507
- PMCID: PMC2895103
- DOI: 10.1073/pnas.1006517107
Probing static disorder in Arrhenius kinetics by single-molecule force spectroscopy
Abstract
The widely used Arrhenius equation describes the kinetics of simple two-state reactions, with the implicit assumption of a single transition state with a well-defined activation energy barrier DeltaE, as the rate-limiting step. However, it has become increasingly clear that the saddle point of the free-energy surface in most reactions is populated by ensembles of conformations, leading to nonexponential kinetics. Here we present a theory that generalizes the Arrhenius equation to include static disorder of conformational degrees of freedom as a function of an external perturbation to fully account for a diverse set of transition states. The effect of a perturbation on static disorder is best examined at the single-molecule level. Here we use force-clamp spectroscopy to study the nonexponential kinetics of single ubiquitin proteins unfolding under force. We find that the measured variance in DeltaE shows both force-dependent and independent components, where the force-dependent component scales with F(2), in excellent agreement with our theory. Our study illustrates a novel adaptation of the classical Arrhenius equation that accounts for the microscopic origins of nonexponential kinetics, which are essential in understanding the rapidly growing body of single-molecule data.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
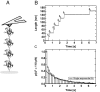
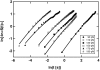
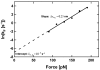
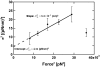
 (Eq. 4). The fit gives
(Eq. 4). The fit gives  and
and  . The measured values of σ2 increase linearly with F2 in this range of forces, in agreement with the prediction of our model.
. The measured values of σ2 increase linearly with F2 in this range of forces, in agreement with the prediction of our model.Similar articles
-
Dwell-time distribution analysis of polyprotein unfolding using force-clamp spectroscopy.Biophys J. 2007 Apr 15;92(8):2896-903. doi: 10.1529/biophysj.106.099481. Epub 2007 Jan 26. Biophys J. 2007. PMID: 17259284 Free PMC article.
-
Direct observation of an ensemble of stable collapsed states in the mechanical folding of ubiquitin.Proc Natl Acad Sci U S A. 2009 Jun 30;106(26):10534-9. doi: 10.1073/pnas.0901213106. Epub 2009 Jun 16. Proc Natl Acad Sci U S A. 2009. PMID: 19541635 Free PMC article.
-
Dynamic disorder can explain non-exponential kinetics of fast protein mechanical unfolding.J Struct Biol. 2017 Jan;197(1):43-49. doi: 10.1016/j.jsb.2016.10.003. Epub 2016 Oct 19. J Struct Biol. 2017. PMID: 27771331
-
Determination of thermodynamics and kinetics of RNA reactions by force.Q Rev Biophys. 2006 Nov;39(4):325-60. doi: 10.1017/S0033583506004446. Epub 2006 Oct 16. Q Rev Biophys. 2006. PMID: 17040613 Free PMC article. Review.
-
Single-molecule studies of protein folding.Annu Rev Biochem. 2008;77:101-25. doi: 10.1146/annurev.biochem.77.060706.093102. Annu Rev Biochem. 2008. PMID: 18412537 Review.
Cited by
-
First passage time distribution in stochastic processes with moving and static absorbing boundaries with application to biological rupture experiments.J Chem Phys. 2010 Jul 21;133(3):034105. doi: 10.1063/1.3456556. J Chem Phys. 2010. PMID: 20649306 Free PMC article.
-
Mechanical Unfolding of Single Polyubiquitin Molecules Reveals Evidence of Dynamic Disorder.ACS Omega. 2020 Apr 15;5(16):9104-9113. doi: 10.1021/acsomega.9b03701. eCollection 2020 Apr 28. ACS Omega. 2020. PMID: 32363262 Free PMC article.
-
Protein nanomechanics in biological context.Biophys Rev. 2021 Aug 7;13(4):435-454. doi: 10.1007/s12551-021-00822-9. eCollection 2021 Aug. Biophys Rev. 2021. PMID: 34466164 Free PMC article. Review.
-
Mechanical unfolding studies of protein molecules.Biophysics (Nagoya-shi). 2012 Feb 17;8:51-58. doi: 10.2142/biophysics.8.51. eCollection 2012. Biophysics (Nagoya-shi). 2012. PMID: 27857607 Free PMC article. Review.
-
Direct observation of chaperone-modulated talin mechanics with single-molecule resolution.Commun Biol. 2022 Apr 4;5(1):307. doi: 10.1038/s42003-022-03258-3. Commun Biol. 2022. PMID: 35379917 Free PMC article.
References
-
- Arrhenius S. On the reaction rate of the inversion of non-refined sugar upon souring. Z Phys Chem. 1889;4:226–248.
-
- Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

