A statistical mechanical theory for a two-dimensional model of water

Abstract

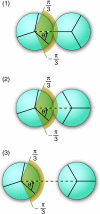
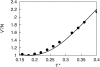
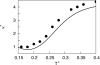
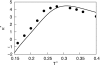
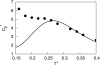
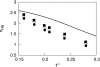
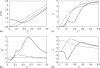
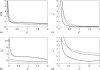
We develop a statistical mechanical model for the thermal and volumetric properties of waterlike fluids. Each water molecule is a two-dimensional disk with three hydrogen-bonding arms. Each water interacts with neighboring waters through a van der Waals interaction and an orientation-dependent hydrogen-bonding interaction. This model, which is largely analytical, is a variant of the Truskett and Dill (TD) treatment of the "Mercedes-Benz" (MB) model. The present model gives better predictions than TD for hydrogen-bond populations in liquid water by distinguishing strong cooperative hydrogen bonds from weaker ones. We explore properties versus temperature T and pressure p. We find that the volumetric and thermal properties follow the same trends with T as real water and are in good general agreement with Monte Carlo simulations of MB water, including the density anomaly, the minimum in the isothermal compressibility, and the decreased number of hydrogen bonds for increasing temperature. The model reproduces that pressure squeezes out water's heat capacity and leads to a negative thermal expansion coefficient at low temperatures. In terms of water structuring, the variance in hydrogen-bonding angles increases with both T and p, while the variance in water density increases with T but decreases with p. Hydrogen bonding is an energy storage mechanism that leads to water's large heat capacity (for its size) and to the fragility in its cagelike structures, which are easily melted by temperature and pressure to a more van der Waals-like liquid state.

Figure 1

The lattice of the model showing both the hexagon of the icelike structure and showing illustrating a pair interaction used for bookkeeping to avoid triple counting.

Figure 2

The three model states: (1) hydrogen bonded, (2) vdW bonded, and (3) nonbonded.

Figure 3

Temperature dependence of the molar volume at p^∗=0.19. Theory (line) vs the Monte Carlo simulation of the MB model (Ref. 55) (symbols).

Figure 4

Temperature dependence of the isothermal compressibility; legend otherwise as for Fig. 3.

Figure 5

Temperature dependence of the thermal expansion coefficient; legend otherwise as for Fig. 3.

Figure 6

Temperature dependence of the heat capacity at constant pressure; legend otherwise as for Fig. 3.

Figure 7

Temperature dependence of the fraction x of hydrogen bonds that are broken; legend otherwise as for Fig. 3.

Figure 8

Temperature dependence of the average number, n_HB, of hydrogen bonds (theory, line), compared to Monte Carlo MB simulations (Ref. 55) for different cutoffs [the cutoffs are 0.5 (filled circles), 0.4 (empty circles), and 0.25(filled squares)].

Figure 9

(a) Temperature dependence of the populations f_i of the different type of hydrogen bonds, at constant pressure, p^∗=0.19. The population of strong hydrogen bonds (long dashed line), weak hydrogen bonds (solid line), and no hydrogen bonds (short dashed line). (b) Experimental populations of OH states in liquid water vs temperature T_r (Ref. 71) along its saturation curve, from IR spectroscopic data [adapted from Fig. 5 of Luck (Ref. 78)]. Temperature here T_r is reduced to critical temperature.

Figure 10

Temperature dependence of the molar volume (a), heat capacity (b), isothermal compressibility (c), and thermal expansion coefficient (d) at p^∗=0.19: theory (solid line), LJ disks (long dashed line), and vdW 2D gas (dashed line).

Figure 11

Pressure dependence of the molar volume (a), heat capacity (b), isothermal compressibility (c), and thermal expansion coefficient (d) at T^∗=0.20; theory (solid line), LJ disks (long dashed line), and vdW 2D gas (dashed line).

Figure 12

(a) Temperature dependence of variance of the hydrogen-bond angle, ⟨θ²⟩ at constant pressure, p^∗=0.19. (b) Pressure dependence of the ⟨θ²⟩ at constant temperature, T^∗=0.20.

Figure 13

(a) Temperature dependence of the variance of volume at constant pressure, p^∗=0.19, and (b) at constant temperature, T^∗=0.20 for the MB model (solid line) and LJ disks (dashed line).