Chemotherapy in conjoint aging-tumor systems: some simple models for addressing coupled aging-cancer dynamics
- PMID: 20550676
- PMCID: PMC2910666
- DOI: 10.1186/1742-4682-7-21
Chemotherapy in conjoint aging-tumor systems: some simple models for addressing coupled aging-cancer dynamics
Abstract
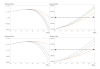
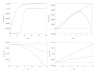
Background: In this paper we consider two approaches to examining the complex dynamics of conjoint aging-cancer cellular systems undergoing chemotherapeutic intervention. In particular, we focus on the effect of cells growing conjointly in a culture plate as a precursor to considering the larger multi-dimensional models of such systems. Tumor cell growth is considered from both the logistic and the Gompertzian case, while normal cell growth of fibroblasts (WI-38 human diploid fibroblasts) is considered as logistic only.
Results: We demonstrate, in a simple approach, how the interdependency of different cell types in a tumor, together with specifications of for treatment, can lead to different evolutionary patterns for normal and tumor cells during a course of therapy.
Conclusions: These results have significance for understanding appropriate pharmacotherapy for elderly patients who are also undergoing chemotherapy.
Figures


Similar articles
-
Modeling the effects of a simple immune system and immunodeficiency on the dynamics of conjointly growing tumor and normal cells.Int J Biol Sci. 2011;7(6):700-7. doi: 10.7150/ijbs.7.700. Epub 2011 Jun 1. Int J Biol Sci. 2011. PMID: 21647303 Free PMC article.
-
Modeling multi-mutation and drug resistance: analysis of some case studies.Theor Biol Med Model. 2017 Mar 21;14(1):6. doi: 10.1186/s12976-017-0052-y. Theor Biol Med Model. 2017. PMID: 28327183 Free PMC article.
-
Modeling drug resistance in a conjoint normal-tumor setting.Theor Biol Med Model. 2015 Jan 15;12:3. doi: 10.1186/1742-4682-12-3. Theor Biol Med Model. 2015. PMID: 25588472 Free PMC article.
-
Sensitivity of latent cancer to chemotherapy.Med Hypotheses. 1992 Jul;38(3):215-6. doi: 10.1016/0306-9877(92)90097-v. Med Hypotheses. 1992. PMID: 1513276 Review.
-
A coming of age for immune checkpoint inhibitors in cancer.Immunotherapy. 2019 Jun;11(8):647-650. doi: 10.2217/imt-2019-0066. Immunotherapy. 2019. PMID: 31088238 Review. No abstract available.
Cited by
-
Modeling the effects of a simple immune system and immunodeficiency on the dynamics of conjointly growing tumor and normal cells.Int J Biol Sci. 2011;7(6):700-7. doi: 10.7150/ijbs.7.700. Epub 2011 Jun 1. Int J Biol Sci. 2011. PMID: 21647303 Free PMC article.
-
Modeling multi-mutation and drug resistance: analysis of some case studies.Theor Biol Med Model. 2017 Mar 21;14(1):6. doi: 10.1186/s12976-017-0052-y. Theor Biol Med Model. 2017. PMID: 28327183 Free PMC article.
-
Modeling drug resistance in a conjoint normal-tumor setting.Theor Biol Med Model. 2015 Jan 15;12:3. doi: 10.1186/1742-4682-12-3. Theor Biol Med Model. 2015. PMID: 25588472 Free PMC article.
-
T model of growth and its application in systems of tumor-immune dynamics.Math Biosci Eng. 2013 Jun;10(3):925-38. doi: 10.3934/mbe.2013.10.925. Math Biosci Eng. 2013. PMID: 23906156 Free PMC article.
References
-
- Witten TM. PhD thesis. State University of New York, Buffalo; 1974. A mathematical model of genetic recombination and its relationship to aging and cancer.
-
- Witten TM. Some mathematics of recombination: Evolution of complexity and genotypic modification in somatic cells-a possible model for aging and cancer effects. Mech Aging and Dev. 1980;13:187–199. - PubMed
-
- Witten TM. Investigating the aging mammalian system: Cellular levels and beyond. Proc 25th Annual Meeting of the Society for General Systems Research, Society for General Systems Research. 1981. pp. 309–315.
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Medical

