The structure of elongated viral capsids

Abstract

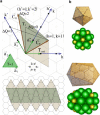
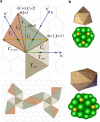
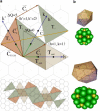
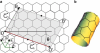
There are many viruses whose genetic material is protected by a closed elongated protein shell. Unlike spherical viruses, the structure and construction principles of these elongated capsids are not fully known. In this article, we have developed a general geometrical model to describe the structure of prolate or bacilliform capsids. We show that only a limited set of tubular architectures can be built closed by hemispherical icosahedral caps. In particular, the length and number of proteins adopt a very special set of discrete values dictated by the axial symmetry (fivefold, threefold, or twofold) and the triangulation number of the caps. The results are supported by experimental observations and simulations of simplified physical models. This work brings about a general classification of elongated viruses that will help to predict their structure, and to design viral cages with tailored geometrical properties for biomedical and nanotechnological applications.

Figure 1

(Color online) (a) Basic elements of the Caspar and Klug construction. The shaded face is a T = 3 (h = k = 1). The icosahedral shell is built by 20 of these triangles. (b) Flat icosahedral template for a T = 3 virus (bottom) and the resulting folded capsid (top). (c) (Top) Example of a T = 7l capsid corresponding to bacteriophage HK97 (22). Arrows indicate the steps along the hexagonal lattice (h = 2,k = 1) from one pentamer to the next. (Bottom) Two triangular faces from the class P = 7l.

Figure 2

(a) (Top) Illustration of Moody's geometrical model for fivefold prolate capsids. (Bottom) Complete flat design of a T_end = 3 and T_mid = Q = 5 prolate capsid, which corresponds to the shell of a φ29 (30). (b) Zenithal (top) and lateral (bottom) views of the folded structure of a T_end = 3 and T_mid = Q = 5 prolate capsid. Below each view, there is a ping-pong model representation of the same capsid, where hexamers are colored in green and pentamers in gold.

Figure 3

The three axes of symmetry of an icosahedron: fivefold (a), threefold (b), and twofold (c and d). The patterned triangles emphasize the end-faces that constitute the cap of the elongated structure. The solid dots highlight the vertexes that define the rim of the caps. In panels c and d, we show that the construction of the twofold prolate is intrinsically skewed and has two possibilities.

Figure 4

(a) (Top) Basic elements to build a prolate based on hemispherical icosahedral caps centered on a threefold axis. The vector ${\overrightarrow{C}}_s={\overrightarrow{C}}_h/3$ (in yellow) joins to consecutive pentamers along the rim of the cap. (Bottom image) Complete flat design of the prolate with the eight end-triangles and the 12 body-triangles. (b) Zenithal (top image) and lateral (bottom image) view of the resulting folded structure, along with its ping-pong model representation. The case illustrated in this figure corresponds to a T_end = 3 and Q_3F = 9.

Figure 5

(a) (Top) Basic elements required to build a prolate capsid with twofold axial symmetry. The vector ${\overrightarrow{C}}_s={\overrightarrow{C}}_h/2$ (in yellow) joins to consecutive pentamers in the rim of the cap. (Bottom) Complete flat design of the prolate with the eight end-triangles and the 12 body-triangles. (b) Zenithal (top image) and lateral (bottom image) view of the resulting folded structure, along with its ping-pong model representation. The case illustrated in this figure corresponds to a T_end = 3 and Q_5F = 14.

Figure 6

(a) The unrolled tubular body of a prolate virus (shaded area) shown on the honeycomb lattice. The solid dots indicate the location of the pentamers in the rim. (b) Tubular body obtained by rolling up the shaded area in the direction of ${\overrightarrow{C}}_h$ so that O meets O′ and B meets B′. The example corresponds to a T_end = 1 and Q_2F = 9 twofold prolate, with h = 1, k = 0, and h′ = 3, k′ = 0.