Mechanism of variable structural colour in the neon tetra: quantitative evaluation of the Venetian blind model

Abstract

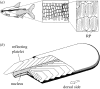
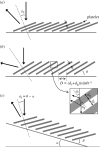
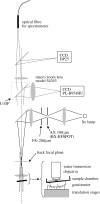
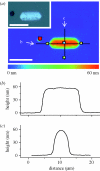
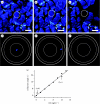
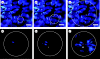
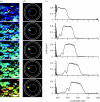
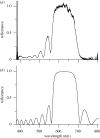
The structural colour of the neon tetra is distinguishable from those of, e.g., butterfly wings and bird feathers, because it can change in response to the light intensity of the surrounding environment. This fact clearly indicates the variability of the colour-producing microstructures. It has been known that an iridophore of the neon tetra contains a few stacks of periodically arranged light-reflecting platelets, which can cause multilayer optical interference phenomena. As a mechanism of the colour variability, the Venetian blind model has been proposed, in which the light-reflecting platelets are assumed to be tilted during colour change, resulting in a variation in the spacing between the platelets. In order to quantitatively evaluate the validity of this model, we have performed a detailed optical study of a single stack of platelets inside an iridophore. In particular, we have prepared a new optical system that can simultaneously measure both the spectrum and direction of the reflected light, which are expected to be closely related to each other in the Venetian blind model. The experimental results and detailed analysis are found to quantitatively verify the model.

Figure 1.

Schematic of the (a) neon tetra and (b) iridophore (reproduced from [15] with permission). The lateral stripe of the neon tetra consists of many iridophores, which are arranged like pavement tiles. Under a higher magnification, it is observed that a single iridophore contains mainly two stacks of the thin light-reflecting platelets (RPs). The nucleus is located in the lower part of the iridophore below the stacks of the platelets.

Figure 2.

Venetian blind model. The longitudinal section of an iridophore is schematically illustrated. There exist many light-reflecting platelets that are tilted at an angle θ with respect to the basal plane of the cell. (a,b) Two different tilt angles. As indicated by a pair of arrows, the spacing between the adjacent platelets is larger in (b) than that in (a). Another difference is noted in the direction of the reflected light. (c) A case when the entire iridophore is tilted by an angle α with respect to the optical axis of the microscope. In fact, our experiments are performed with non-zero α so that the reflected light appears around the centre of the far-field pattern. The inset in (b) shows the definitions of the parameters of the multilayer interference phenomenon. The thicknesses (refraction angle) of the guanine platelet and cytoplasm part are denoted by d_g (ϕ_g) and d_c (ϕ_c), respectively. Further, a constant parameter D = (d_g + d_c)/sinθ is introduced to represent the distance between two adjacent platelets located on the bottom (or top) surface of the stack.

Figure 3.

Optical system of a microscope that functions both as a microspectrophotometer and as a microscatterometer. Light from a Xe lamp is focused on a 100 µm diameter pinhole placed in the plane of the aperture stop (AS). The pinhole is imaged on the back focal plane of the objective lens so that the illuminating light becomes nearly collimated at the sample position. The real image of the sample is observed with a CCD camera (DP25). Using an optical fibre, the reflected light from a small part is guided into a spectrometer. Another CCD camera (PL-B954HU) observes the intensity pattern of the back focal plane of the objective lens through a beam splitter inside the dual-port unit (U-DP) and a macro zoom lens (model 54 363). A pinhole of a 200 µm diameter is placed in the plane of field stop (FS) to restrict the illuminated area during the measurements. The lower right illustration shows that the sample chamber is placed on the goniometer attached to translation stages.

Figure 4.

The profile of a single light-reflecting platelet. (a) A colour image created by the height data obtained by using an interference microscope. The inset shows the same platelet observed by a normal optical microscope under epi-illumination (scale bar, 10 µm). The height profiles are shown in (b,c), which are obtained along the longitudinal and cross sections, respectively, as indicated by the corresponding letters in (a).

Figure 5.

Tilt angle dependence of the real image and the far-field pattern of the iridophores. By using the goniometer, the sample chamber is tilted through angles of 0° (a,d), 12° (b,e), and 22° (c,f). Photographs (a–c) show the real image of the same part, in which several iridophores containing many blue stacks of the platelets are shown (scale bar, 20 µm). The white circle shows the illuminated area when the far-field patterns are observed. The images (d–f) are the observed far-field patterns corresponding to (a–c). As the sample is tilted, the spot laterally moves as shown in (e) and goes out of the observable angular range in (f). The two inner dotted circles indicate the angles of 15° and 30° with respect to the optical axis of the microscope (the centre of the far-field pattern), and the solid circle indicates the maximum angle 35.7° of the detectable angular range. The plot (g) shows the relation between the tilt angle of the goniometer and the change in the angle of reflection. The line is drawn according to the general relation in specular reflection: the reflection angle is twice the tilt angle.

Figure 6.

Illuminated area dependence of the far-field pattern. (a–c) The same photograph of the real image of several iridophores. The white circle shows the illuminated area when the corresponding far-field patterns (d–f) are observed. (d–f) The white circle indicates the maximum angle of 35.7° of the detectable range. The experimental artefact of a white spot is noted in (e,f), which originates from the back surface of the objective. Scale bar, 20 µm in (a–c).

Figure 7.

Optical properties of the iridophore during colour change from blue to yellow. (a) Real image of the iridophore during the colour change. The red circle indicates the illuminated area for the measurements shown in (b,c) (scale bar, 20 µm). (b) The far-field patterns obtained corresponding to the real images shown in (a). The two inner dotted circles indicate the angles of 15° and 30° with respect to the optical axis, and the solid circle indicates the maximum angle 35.7° of the detectable angular range. (c) The reflectance spectra obtained corresponding to the images in (a,b).

Figure 8.

Experimentally obtained relation between the centre wavelength λ_c of the rectangular component in the spectrum and the tilt angle θ of the platelets. The results of two measurements for two different iridophores are shown by triangles and circles. The curves are drawn according to relation (1) for the parameters D = 500, 570, 670, 800, and 1100 nm from the top to bottom. The parameter value α = 11.3° is used, except for the curve with D = 570 nm where α is 12.0°. See text for the other parameters. When the shorter wavelength edge of the rectangular component cannot be observed owing to the limitation on the spectral range, λ_c is determined from the edge of the longer wavelength side and the approximate half width of the rectangular component that is estimated from other spectra.

Figure 9.

(a) Example of an experimentally obtained reflectance spectrum from a small part of a yellow-coloured stack. (b) Theoretical reflectance spectrum calculated with the parameters d_g = 60 nm and d_c = 155 nm. These thicknesses are selected so as to satisfy the constructive interference condition at a wavelength of 625 nm with refractive indices n_g = 1.83 and n_c = 1.37 and an incidence angle of 15°. The number of guanine platelets is assumed to be 12. Since the incidence angle is not normal, reflectance depends on the light polarization. The reflectance spectra calculated for two perpendicular polarizations are averaged, since the incident light is assumed to be unpolarized.