3D finite compartment modeling of formation and healing of bruises may identify methods for age determination of bruises

Abstract

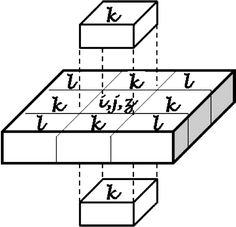
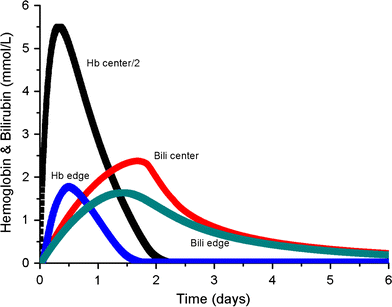
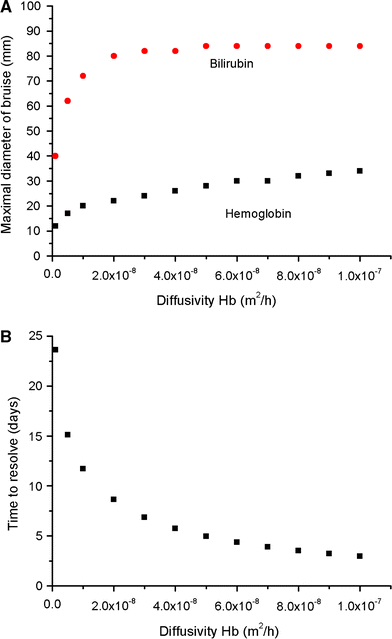
Simulating the spatial and temporal behavior of bruises may identify methods that allow accurate age determination of bruises to assess child abuse. We developed a numerical 3D model to simulate the spatial kinetics of hemoglobin and bilirubin during the formation and healing of bruises. Using this model, we studied how skin thickness, bruise diameter and diffusivities affect the formation and healing of circular symmetric bruises and compared a simulated bruise with a natural inhomogeneous bruise. Healing is faster for smaller bruises in thinner and less dense skin. The simulated and natural bruises showed similar spatial and temporal dynamics. The different spatio-temporal dynamics of hemoglobin and bilirubin allows age determination of model bruises. Combining our model predictions with individual natural bruises may allow optimizing our model parameters. It may particularly identify methods for more accurate age determination than currently possible to aid the assessment of child abuse.

Fig. 1

a The skin model consists of 3 layers, the top layer of the dermis, the bottom layer of the dermis and the subcutaneous fat layer. Each layer consists of 100 × 100 compartmets (for ease of presentation a smaller number is shown). b and c A pool of hemoglobin is defined in the subcutaneous layer. Via Michealis–Menten kinetics the hemoglobin is converted into bilirubin. Both hemoglobin and bilirubin flow inside the layers and between the layers

Fig. 2

The average of adjacent compartments k and across compartments l are used in the calculations

Fig. 3

Kinetics in bruise in center and at 8 mm from center. The concentration of hemoglobin in the center in the graph is divided by 2, to display all chromophores more clearly in 1 graph. The simulations are done with the standard parameters as given in Table 1

Fig. 4

a Final diameter of bruise for different diffusivities. b Time to resolve for different diffusivities. D _Hb was varied between 1 × 10⁻⁸–8 × 10⁻⁸ m²/h, D _B remained 4 × D _Hb and was varied between 4 × 10⁻⁸–3.2 × 10⁻⁷ m²/h. The simulations are done with the standard parameters as given in Table 1, except diffusivity

Fig. 5

a Final diameter of bruise for different dermal thicknesses. b Time to resolve for different dermal thicknesses. Thickness varied between 1–2 mm. The simulations are done with the standard parameters as given in Table 1, except dermal thickness

Fig. 6

a Final diameter of the bruise for different starting diameters. b Diameter of hemoglobin area of bruise over time for different starting diameters (the steps in the hemoglobin kinetics are due to the resolution of the model). c Ratio of the diameter of the area containing hemoglobin over the diameter of the area containing bilirubin for different starting diameters. The simulations are done with the standard parameters as given in Table 1, except for the starting diameter. d Combining Fig. 6b, c: diameter of the hemoglobin area (gray). Ratios of hemoglobin over bilirubin (color)

Fig. 7

a Non homogeneous natural bruise photographed on 3 different days (cross sect. 40 mm). Ballpoint stripes were drawn for orientation. b Simulations of a non homogeneous bruise (starting blood pool extracted from photo day 1) Dermal thickness = 1000 μm, D _Hb 1.6 × 10⁻⁹ m²/h, D _B 6.4 × 10⁻⁹ m²/h, τ_B 100 h, concentration HO = 10.5 mg/l. Ballpoint stripes were placed on the same location for comparison

Fig. 8

a Total area of hemoglobin area of the simulated and natural bruise. b Total bilirubin area of the simulated and natural bruise