Theory for polymer analysis using nanopore-based single-molecule mass spectrometry
- PMID: 20566890
- PMCID: PMC2901474
- DOI: 10.1073/pnas.1002194107
Theory for polymer analysis using nanopore-based single-molecule mass spectrometry
Abstract
Nanometer-scale pores have demonstrated potential for the electrical detection, quantification, and characterization of molecules for biomedical applications and the chemical analysis of polymers. Despite extensive research in the nanopore sensing field, there is a paucity of theoretical models that incorporate the interactions between chemicals (i.e., solute, solvent, analyte, and nanopore). Here, we develop a model that simultaneously describes both the current blockade depth and residence times caused by individual poly(ethylene glycol) (PEG) molecules in a single alpha-hemolysin ion channel. Modeling polymer-cation binding leads to a description of two significant effects: a reduction in the mobile cation concentration inside the pore and an increase in the affinity between the polymer and the pore. The model was used to estimate the free energy of formation for K(+)-PEG inside the nanopore (approximately -49.7 meV) and the free energy of PEG partitioning into the nanopore ( approximately 0.76 meV per ethylene glycol monomer). The results suggest that rational, physical models for the analysis of analyte-nanopore interactions will develop the full potential of nanopore-based sensing for chemical and biological applications.
Conflict of interest statement
Conflict of interest statement: J.W.F.R. and J.J.K. have filed a provisional patent for single-molecule sizing with a nanopore. J.E.R., J.J.K., and J.W.F.R. are filing a provisional patent for aspects of the work in this manuscript.
Figures



 , and viscous force
, and viscous force  on the entire PEG molecule. When mb bound cations dissociate from the complex with a corresponding change in free energy, mbΔGo,pore, PEG exits the nanopore with a change in free energy nΔGc. The total change in the free energy resulting from the exodus of PEG from the nanopore, used in Eq. 8, comes from the combination of the two steps highlighted by the blue arrow.
on the entire PEG molecule. When mb bound cations dissociate from the complex with a corresponding change in free energy, mbΔGo,pore, PEG exits the nanopore with a change in free energy nΔGc. The total change in the free energy resulting from the exodus of PEG from the nanopore, used in Eq. 8, comes from the combination of the two steps highlighted by the blue arrow.
 calculated from current blockades measured at four different applied potentials [-40 mV (green), -50 mV (orange), -60 mV (blue), and -70 mV (red)], but with Vapp held fixed at -40 mV in Eq. 2, show the explicit voltage dependence of the blockade amplitudes. (C) However, when the actual voltages are used in the model, the normalized residuals converge
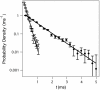
calculated from current blockades measured at four different applied potentials [-40 mV (green), -50 mV (orange), -60 mV (blue), and -70 mV (red)], but with Vapp held fixed at -40 mV in Eq. 2, show the explicit voltage dependence of the blockade amplitudes. (C) However, when the actual voltages are used in the model, the normalized residuals converge  . (D) Experimentally determined PEG residence times in the nanopore (open circles) and least-squares fits from Eq. 8 (solid lines) along with normalized residuals above. The data and fits correspond to Vapp values of -40 mV (green), -50 mV (orange), -60 mV (blue), and -70 mV (red) for each plot. (E) Normalized residuals between the residence time data and model (Eq. 8).
. (D) Experimentally determined PEG residence times in the nanopore (open circles) and least-squares fits from Eq. 8 (solid lines) along with normalized residuals above. The data and fits correspond to Vapp values of -40 mV (green), -50 mV (orange), -60 mV (blue), and -70 mV (red) for each plot. (E) Normalized residuals between the residence time data and model (Eq. 8).Similar articles
-
Single polymer molecules in a protein nanopore in the limit of a strong polymer-pore attraction.Phys Rev Lett. 2006 Jul 7;97(1):018301. doi: 10.1103/PhysRevLett.97.018301. Epub 2006 Jul 5. Phys Rev Lett. 2006. PMID: 16907416
-
Partitioning of individual flexible polymers into a nanoscopic protein pore.Biophys J. 2003 Aug;85(2):897-910. doi: 10.1016/S0006-3495(03)74529-9. Biophys J. 2003. PMID: 12885637 Free PMC article.
-
Pore-forming toxins as tools for polymer analytics: From sizing to sequencing.Methods Enzymol. 2021;649:587-634. doi: 10.1016/bs.mie.2021.01.017. Epub 2021 Feb 19. Methods Enzymol. 2021. PMID: 33712201
-
Nanopore sequencing technology: nanopore preparations.Trends Biotechnol. 2007 Apr;25(4):174-81. doi: 10.1016/j.tibtech.2007.02.008. Epub 2007 Feb 22. Trends Biotechnol. 2007. PMID: 17320228 Review.
-
Probing protein nanopores with poly(ethylene glycol)s.Proteomics. 2022 Mar;22(5-6):e2100055. doi: 10.1002/pmic.202100055. Epub 2022 Jan 24. Proteomics. 2022. PMID: 35030301 Review.
Cited by
-
Polymers pushing Polymers: Polymer Mixtures in Thermodynamic Equilibrium with a Pore.Macromolecules. 2012 Nov 13;45(21):8921-8928. doi: 10.1021/ma3017508. Epub 2012 Oct 19. Macromolecules. 2012. PMID: 23226877 Free PMC article.
-
Protein identification by nanopore peptide profiling.Nat Commun. 2021 Oct 4;12(1):5795. doi: 10.1038/s41467-021-26046-9. Nat Commun. 2021. PMID: 34608150 Free PMC article.
-
Nanopore Detection Assisted DNA Information Processing.Nanomaterials (Basel). 2022 Sep 9;12(18):3135. doi: 10.3390/nano12183135. Nanomaterials (Basel). 2022. PMID: 36144924 Free PMC article. Review.
-
Laser-based temperature control to study the roles of entropy and enthalpy in polymer-nanopore interactions.Sci Adv. 2021 Apr 21;7(17):eabf5462. doi: 10.1126/sciadv.abf5462. Print 2021 Apr. Sci Adv. 2021. PMID: 33883140 Free PMC article.
-
Characterizing and controlling the motion of ssDNA in a solid-state nanopore.Biophys J. 2011 Nov 2;101(9):2214-22. doi: 10.1016/j.bpj.2011.08.038. Epub 2011 Nov 1. Biophys J. 2011. PMID: 22067161 Free PMC article.
References
-
- Di Marzio E. Profound implications for biophysics of the polymer threading a membrane transition. In: Kasianowicz JJ, Kellermayer MSZ, Deamer DW, editors. Structure and Dynamics of Confined Polymers. Vol 87. The Netherlands: Kluwer, Dordrecht; 2002. pp. 1–22.
-
- Forrest S. The path to ubiquitous and low-cost organic electronic appliances on plastic. Nature. 2004;428:911–918. - PubMed
-
- Granick S, et al. Macromolecules at surfaces: Research challenges and opportunities from tribology to biology. J Polym Sci Pol Phys. 2003;41:2755–2793.
-
- Gay C, deGennes P, Raphaël E, Brochard-Wyart F. Injection threshold for a statistically branched polymer inside a nanopore. Macromolecules. 1996;29:8379–8382.
-
- Barbara PF, Chang W, Link S, Scholes GD, Yethiraj A. Structure and dynamics of conjugated polymers in liquid crystalline solvents. Ann Rev Phys Chem. 2007;58:565–584. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

