Modeling bistable cell-fate choices in the Drosophila eye: qualitative and quantitative perspectives
- PMID: 20570936
- PMCID: PMC2889600
- DOI: 10.1242/dev.044826
Modeling bistable cell-fate choices in the Drosophila eye: qualitative and quantitative perspectives
Abstract
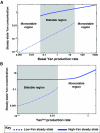
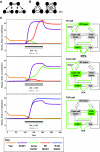
A major goal of developmental biology is to understand the molecular mechanisms whereby genetic signaling networks establish and maintain distinct cell types within multicellular organisms. Here, we review cell-fate decisions in the developing eye of Drosophila melanogaster and the experimental results that have revealed the topology of the underlying signaling circuitries. We then propose that switch-like network motifs based on positive feedback play a central role in cell-fate choice, and discuss how mathematical modeling can be used to understand and predict the bistable or multistable behavior of such networks.
Figures





Similar articles
-
The Hippo pathway effector Yki downregulates Wg signaling to promote retinal differentiation in the Drosophila eye.Development. 2015 Jun 1;142(11):2002-13. doi: 10.1242/dev.117358. Epub 2015 May 14. Development. 2015. PMID: 25977365 Free PMC article.
-
A mathematical model for apoptotic switch in Drosophila.Phys Biol. 2015 Aug 20;12(5):056003. doi: 10.1088/1478-3975/12/5/056003. Phys Biol. 2015. PMID: 26291171
-
Binary cell fate decisions and fate transformation in the Drosophila larval eye.PLoS Genet. 2013;9(12):e1004027. doi: 10.1371/journal.pgen.1004027. Epub 2013 Dec 26. PLoS Genet. 2013. PMID: 24385925 Free PMC article.
-
Gene regulatory networks during the development of the Drosophila visual system.Curr Top Dev Biol. 2020;139:89-125. doi: 10.1016/bs.ctdb.2020.02.010. Epub 2020 Apr 7. Curr Top Dev Biol. 2020. PMID: 32450970 Free PMC article. Review.
-
Modeling ncRNA-Mediated Circuits in Cell Fate Decision.Methods Mol Biol. 2019;1912:411-426. doi: 10.1007/978-1-4939-8982-9_16. Methods Mol Biol. 2019. PMID: 30635903 Review.
Cited by
-
A bistable autoregulatory module in the developing embryo commits cells to binary expression fates.Curr Biol. 2023 Jul 24;33(14):2851-2864.e11. doi: 10.1016/j.cub.2023.06.060. Epub 2023 Jul 14. Curr Biol. 2023. PMID: 37453424 Free PMC article.
-
Dissection of a Krox20 positive feedback loop driving cell fate choices in hindbrain patterning.Mol Syst Biol. 2013;9:690. doi: 10.1038/msb.2013.46. Mol Syst Biol. 2013. PMID: 24061538 Free PMC article.
-
Polycomb group genes are required to maintain a binary fate choice in the Drosophila eye.Neural Dev. 2015 Jan 31;10:2. doi: 10.1186/s13064-015-0029-7. Neural Dev. 2015. PMID: 25636358 Free PMC article.
-
Evolution of hierarchy and irreversibility in theoretical cell differentiation model.PNAS Nexus. 2023 Dec 22;3(1):pgad454. doi: 10.1093/pnasnexus/pgad454. eCollection 2024 Jan. PNAS Nexus. 2023. PMID: 38205032 Free PMC article.
-
Modeling the epigenetic attractors landscape: toward a post-genomic mechanistic understanding of development.Front Genet. 2015 Apr 23;6:160. doi: 10.3389/fgene.2015.00160. eCollection 2015. Front Genet. 2015. PMID: 25954305 Free PMC article. Review.
References
-
- Amonlirdviman K., Khare N. A., Tree D. R. P., Chen W.-S., Axelrod J. D., Tomlin C. J. (2005). Mathematical modeling of planar cell polarity to understand domineering nonautonomy. Science 307, 423-426 - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

