A modular gradient-sensing network for chemotaxis in Escherichia coli revealed by responses to time-varying stimuli
- PMID: 20571531
- PMCID: PMC2913400
- DOI: 10.1038/msb.2010.37
A modular gradient-sensing network for chemotaxis in Escherichia coli revealed by responses to time-varying stimuli
Abstract
The Escherichia coli chemotaxis-signaling pathway computes time derivatives of chemoeffector concentrations. This network features modules for signal reception/amplification and robust adaptation, with sensing of chemoeffector gradients determined by the way in which these modules are coupled in vivo. We characterized these modules and their coupling by using fluorescence resonance energy transfer to measure intracellular responses to time-varying stimuli. Receptor sensitivity was characterized by step stimuli, the gradient sensitivity by exponential ramp stimuli, and the frequency response by exponential sine-wave stimuli. Analysis of these data revealed the structure of the feedback transfer function linking the amplification and adaptation modules. Feedback near steady state was found to be weak, consistent with strong fluctuations and slow recovery from small perturbations. Gradient sensitivity and frequency response both depended strongly on temperature. We found that time derivatives can be computed by the chemotaxis system for input frequencies below 0.006 Hz at 22 degrees C and below 0.018 Hz at 32 degrees C. Our results show how dynamic input-output measurements, time honored in physiology, can serve as powerful tools in deciphering cell-signaling mechanisms.
Conflict of interest statement
The authors declare that they have no conflict of interest.
Figures
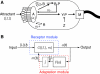

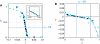
 ; see text for interpretation of parameters. Source data is available for this figure at
; see text for interpretation of parameters. Source data is available for this figure at 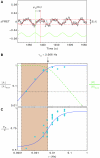
 (A) with a frequency ν equal to that of the applied stimulus (green line), and the fit by a sinusoid (red line) of the form a(t)=a0+∣A∣cos(2πνt−φD), where ∣A∣ is the amplitude of the response and φD is the phase delay. When the amplitude (B) and phase (C) of responses are plotted against the driving frequency ν, the data are in excellent agreement with the analytical solutions of our model (equations (13) and (14)), plotted here without any free-fitting parameters—the solution uses parameters obtained separately from the ramp-response experiments of Figure 2 and 3 and MWC-model parameters obtained separately in dose–response experiments using step stimuli. These analytical solutions define the characteristic frequency of the response νm≈0.006 Hz, below which the network is able to compute time derivatives. The dashed green curve in (B) is the derivative-filtering function ∣H∣ obtained by factoring the solution of our linearized model (equation (15)). The characteristic frequency, νm determines the upper boundary of the frequency band over which time derivatives can be computed (shaded region). Presumably, the lower boundary would be determined by a noise floor, which in this figure is taken arbitrarily to be where the response amplitude (black curve in B) falls below 5% of maximum. Source data is available for this figure at
(A) with a frequency ν equal to that of the applied stimulus (green line), and the fit by a sinusoid (red line) of the form a(t)=a0+∣A∣cos(2πνt−φD), where ∣A∣ is the amplitude of the response and φD is the phase delay. When the amplitude (B) and phase (C) of responses are plotted against the driving frequency ν, the data are in excellent agreement with the analytical solutions of our model (equations (13) and (14)), plotted here without any free-fitting parameters—the solution uses parameters obtained separately from the ramp-response experiments of Figure 2 and 3 and MWC-model parameters obtained separately in dose–response experiments using step stimuli. These analytical solutions define the characteristic frequency of the response νm≈0.006 Hz, below which the network is able to compute time derivatives. The dashed green curve in (B) is the derivative-filtering function ∣H∣ obtained by factoring the solution of our linearized model (equation (15)). The characteristic frequency, νm determines the upper boundary of the frequency band over which time derivatives can be computed (shaded region). Presumably, the lower boundary would be determined by a noise floor, which in this figure is taken arbitrarily to be where the response amplitude (black curve in B) falls below 5% of maximum. Source data is available for this figure at 



References
-
- Alon U (2007) An Introduction to Systems Biology. Boca Raton, FL: CRC Press
-
- Alon U, Surette MG, Barkai N, Leibler S (1999) Robustness in bacterial chemotaxis. Nature 397: 168–171 - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

