Slope-based stochastic resonance: how noise enables phasic neurons to encode slow signals
- PMID: 20585612
- PMCID: PMC2891698
- DOI: 10.1371/journal.pcbi.1000825
Slope-based stochastic resonance: how noise enables phasic neurons to encode slow signals
Abstract
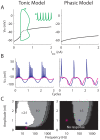
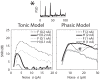
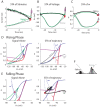
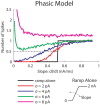
Fundamental properties of phasic firing neurons are usually characterized in a noise-free condition. In the absence of noise, phasic neurons exhibit Class 3 excitability, which is a lack of repetitive firing to steady current injections. For time-varying inputs, phasic neurons are band-pass filters or slope detectors, because they do not respond to inputs containing exclusively low frequencies or shallow slopes. However, we show that in noisy conditions, response properties of phasic neuron models are distinctly altered. Noise enables a phasic model to encode low-frequency inputs that are outside of the response range of the associated deterministic model. Interestingly, this seemingly stochastic-resonance (SR) like effect differs significantly from the classical SR behavior of spiking systems in both the signal-to-noise ratio and the temporal response pattern. Instead of being most sensitive to the peak of a subthreshold signal, as is typical in a classical SR system, phasic models are most sensitive to the signal's rising and falling phases where the slopes are steep. This finding is consistent with the fact that there is not an absolute input threshold in terms of amplitude; rather, a response threshold is more properly defined as a stimulus slope/frequency. We call the encoding of low-frequency signals with noise by phasic models a slope-based SR, because noise can lower or diminish the slope threshold for ramp stimuli. We demonstrate here similar behaviors in three mechanistic models with Class 3 excitability in the presence of slow-varying noise and we suggest that the slope-based SR is a fundamental behavior associated with general phasic properties rather than with a particular biological mechanism.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


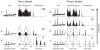



References
-
- Longtin A. Stochastic resonance in neuron models. J Stat Phys. 1993;70:309–327.
-
- Moss F, Douglass JK, Wilkens L, Pierson D, Pantazelou E. Stochastic Resonance in an Electronic FitzHugh-Nagumo Model. In: Buchler JR, Kandrup HE, editors. Stochastic Processes in Astrophysics. New York: The New York Academy of Sciences; 1993. pp. 26–41.
-
- Braun HA, Wissing H, Schafer K, Hirsch MC. Oscillation and noise determine signal transduction in shark multimodal sensory cells. Nature. 1994;367:270–273. - PubMed
-
- Wiesenfeld K, Moss F. Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs. Nature. 1995;373:33–36. - PubMed
-
- Cordo P, et al. Noise in human muscle spindles. Nature. 1996;383:769–770. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
Miscellaneous

