Enhanced sampling and applications in protein folding in explicit solvent

Abstract

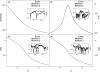
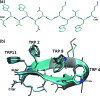
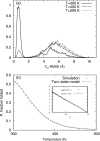
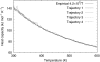
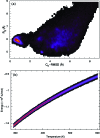
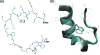
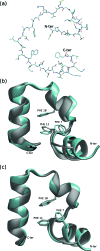
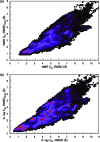
We report a single-copy tempering method for simulating large complex systems. In a generalized ensemble, the method uses runtime estimate of the thermal average energy computed from a novel integral identity to guide a continuous temperature-space random walk. We first validated the method in a two-dimensional Ising model and a Lennard-Jones liquid system. It was then applied to folding of three small proteins, trpzip2, trp-cage, and villin headpiece in explicit solvent. Within 0.5-1 microsecond, all three systems were reversibly folded into atomic accuracy: the alpha carbon root mean square deviations of the best folded conformations from the native states were 0.2, 0.4, and 0.4 A, for trpzip2, trp-cage, and villin headpiece, respectively.

Figure 1

(a) Schematic illustration of auxiliary functions ϕ(β), ϕ_s(β) and ϕ_t(β), which are used in the integral identity for estimating the thermal average energy $\tilde{E}\left(\beta \right)$. The estimate computed in this way uses statistics from a large temperature window (β₋,β₊) instead of a single bin (β_i,β_i+1) and also avoids systematic bias. ϕ(β) is a combination of a smooth function ϕ_s(β) and a function ϕ_t(β) localized at (β_i,β_i+1). ϕ_s(β) is controlled by two parameters a₊ and a₋ that satisfy a₊+a₋=1. (b) Schematic illustration of ${\varphi }_s^{\prime }\left(\beta \right)$ and $-{\varphi }_t^{\prime }\left(\beta \right)$. ${\varphi }_s^{\prime }\left(\beta \right)$ (shaded) spans over the whole temperature window (β₋,β₊) while $-{\varphi }_t^{\prime }\left(\beta \right)$ is localized in (β_i,β_i+1).

Figure 2

Thermodynamic quantities as functions of β for the 32×32 Ising model. Results from the method introduced in Sec. 2 are labeled as method 1 (thin solid lines, cross for errors), and those from the method introduced in Appendix B are labeled as method 2 (dashed lines, circles for errors); (a) the partition function, (b) the heat capacity, (c) the average energy, and (d) $\tilde{E}\left(\beta \right)$.

Figure 3

Reconstructed energy distribution at a few temperatures using Eq. 20 with a window size Δβ=0.02 for the 32×32 Ising model. For comparison, we also show the resulting distributions from averaging energy distributions of two adjacent temperature bins, with the bin size δβ=0.0002. The energy distributions constructed from Eq. 20 with a larger window are more precise than those from simple averages of two adjacent bins.

Figure 4

(a) $\tilde{E}\left(\beta \right)$ of an 864-particle Lennard-Jones system. As a comparison, the values of the average energy from several constant temperature simulations are shown as dots. (b) The reconstructed radial distribution functions of an 864-particle Lennard-Jones system at two selected temperatures T=1.0 and 2.0 are shown as points. As a comparison, the corresponding radial distribution functions from independent constant temperature simulations are shown as lines.

Figure 5

Trpzip2: (a) the initial fully extended conformation, (b) a typical folded structure from trajectory 2. The C_α-RMSD and heavy atom RMSD are 0.25 and 1.08 Å, respectively. Gray: reference structure (PDB ID: 1LE1).

Figure 6

Trpzip2: quantities along two independent simulation trajectories. Left: the first 200 ns of a fast-folding trajectory (trajectory 1). Right: 2 μs of trajectory 3. Panels from top to bottom: (a) C_α-RMSD from native structure, (b) C_α radius of gyration, (c) temperature, and (d) potential energy.

Figure 7

Trpzip2: (a) distribution along the RMSD from the native structure at three temperatures 300, 400, and 500 K, calculated from trajectory 3 and (b) fraction P of the folded state vs the temperature. Inset: linear fitting of log(P₀∕P−1) vs β according to the two-state model.

Figure 8

Trpzip2: the heat capacity, computed from four independent trajectories. Bold solid line: empirical formula C_V≈4.2×10³∕T.

Figure 9

Trpzip2: joint distributions of (a) the radius of gyration vs C_α-RMSD and (b) the potential energy vs temperature. A brighter color represents a higher population density.

Figure 10

Trp-cage: (a) the initial fully extended structure, (b) a typical folded structure. The C_α-RMSD and the all heavy atom RMSD are 0.44 and 1.54 Å, respectively. Gray: reference structure (PDB ID: 1L2Y).

Figure 11

Trp-cage: three independent trajectories (a) C_α-RMSD from native structure, (b) C_α radius of gyration, (c) temperature, and (d) potential energy.

Figure 12

Villin headpiece: (a) the initial fully extended structure, (b) a typical folded structure compared with an NMR reference structure (gray, PDB ID: 1VII, C_α-RMSD: 1.15 Å), (c) a typical folded structure compared with an x-ray structure (gray, PDB ID: 1YRF, C_α-RMSD: 0.47 Å), and the N-terminal is not shown due to the sequence difference.

Figure 13

Villin headpiece: joint distributions of (a) C_α-RMSD and C_α-RMSD_core (from residues 9∼32) using the NMR structure as the reference and (b) C_α-RMSD and C_α-RMSD_core, using the x-ray structure as the reference. Statistics from the two trajectories were combined.