Beyond co-localization: inferring spatial interactions between sub-cellular structures from microscopy images

Abstract

Background: Sub-cellular structures interact in numerous direct and indirect ways in order to fulfill cellular functions. While direct molecular interactions crucially depend on spatial proximity, other interactions typically result in spatial correlations between the interacting structures. Such correlations are the target of microscopy-based co-localization analysis, which can provide hints of potential interactions. Two complementary approaches to co-localization analysis can be distinguished: intensity correlation methods capitalize on pattern discovery, whereas object-based methods emphasize detection power.

Results: We first reinvestigate the classical co-localization measure in the context of spatial point pattern analysis. This allows us to unravel the set of implicit assumptions inherent to this measure and to identify potential confounding factors commonly ignored. We generalize object-based co-localization analysis to a statistical framework involving spatial point processes. In this framework, interactions are understood as position co-dependencies in the observed localization patterns. The framework is based on a model of effective pairwise interaction potentials and the specification of a null hypothesis for the expected pattern in the absence of interaction. Inferred interaction potentials thus reflect all significant effects that are not explained by the null hypothesis. Our model enables the use of a wealth of well-known statistical methods for analyzing experimental data, as demonstrated on synthetic data and in a case study considering virus entry into live cells. We show that the classical co-localization measure typically under-exploits the information contained in our data.

Conclusions: We establish a connection between co-localization and spatial interaction of sub-cellular structures by formulating the object-based interaction analysis problem in a spatial statistics framework based on nearest-neighbor distance distributions. We provide generic procedures for inferring interaction strengths and quantifying their relative statistical significance from sets of discrete objects as provided by image analysis methods. Within our framework, an interaction potential can either refer to a phenomenological or a mechanistic model of a physico-chemical interaction process. This increased flexibility in designing and testing different hypothetical interaction models can be used to quantify the parameters of a specific interaction model or may catalyze the discovery of functional relations.

Figure 1

Illustration of co-localization analysis and cellular context. (A) Illustration of co-localization analysis based on nearest neighbor distances (arrows) between point-like objects (dots) and circular objects (solid circles). For all distances d, the state density q(d) is proportional to the total length of the d-isoline (dashed lines) in Ω. The expected co-localization in the absence of interactions, , is proportional to the area enclosed by the t-isoline (gray region). (B)-(D) Effect of the positioning of the objects Y on q(d), illustrating the influence of the cellular context.

Figure 2

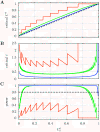
Power analysis for a step potential. Minimum C^t (A) and (B) that allows rejecting H₀: "no interaction" (α = 0.05) as a function of the base-level . In A, the expected value of C^t under H₀ is indicated by a dashed line. (C) Statistical power (1 - β) for detecting interactions of a true strength ϵ = 1. Red, green, and blue lines correspond to N = 10, 100, and 1000, respectively, in all three panels.

Figure 3

Power analysis for non-step potentials. (A) Black line: state density q(d) for M = 100 circular objects Y with radius R = 3.57 randomly placed in a square domain of size 200 × 200; R is chosen to yield a circle-covered area fraction of 0.1; Colored lines: resulting distance distribution p(d) for the three potentials shown in B. (B) Plummer potential (Eq. 12) with ϵ = 1 and varying scale parameter. (C) Monte-Carlo estimates of 80%-power isolines in the N-a-plane; dashed lines: tests based on T^st, solid lines: tests based on T^pl. Note that larger kinks in the dashed lines are due to the discreteness of T^st and are statistically significant. Colors in A-C indicate scale parameters of the true potential; red: σ = 0.2, green: σ = 1.0, and blue: σ = 5.0.

Figure 4

Non-parametric estimate of the interaction potential. The non-parametric estimate of the interaction potential based on all imaged cells.

Figure 5

Interaction analysis applied to virus trafficking. Interaction analysis for a single cell infected with TS1, imaged 27 min post infection. (A) Imaged endosomes (Rab5-EGFP) with overlaid outlines (solid red lines) and virus centroid positions (blue crosses, virus channel not shown). Nearest-endosome-distance isolines (dashed red lines) are shown in the magnified inset. (B) State density q(d) for the shown cell (dashed black line), observed virus-to-nearest-endosome distances (marks and histogram, N = 143), and estimated distance distribution from the model p(d) (solid black line). 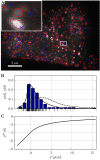(C) Estimated Hermquist potential ( = 3.90, = 3.96) of the interactions between viruses and nearest endosomes.

Figure 6

Time-resolved interaction analysis of the trafficking of two strains of viruses. Estimated strength of a Hermquist potential (scale σ* = 3.96) for the interaction between endosomes and virus particles versus the time post infection. Red circles: TS1; blue crosses: Ad2. The time course of the mean (solid lines) and the ± 1 standard deviation interval (shaded bands) are estimated using a Nadaraya-Watson kernel estimator with bandwidth of 5 min.