Topological basis for the robust distribution of blood to rodent neocortex

Abstract

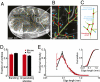
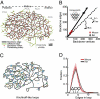
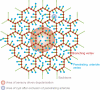
The maintenance of robust blood flow to the brain is crucial to the health of brain tissue. We examined the pial network of the middle cerebral artery, which distributes blood from the cerebral arteries to the penetrating arterioles that source neocortical microvasculature, to characterize how vascular topology may support such robustness. For both mice and rats, two features dominate the topology. First, interconnected loops span the entire territory sourced by the middle cerebral artery. Although the loops comprise <10% of all branches, they maintain the overall connectivity of the network after multiple breaks. Second, >80% of offshoots from the loops are stubs that end in a single penetrating arteriole, as opposed to trees with multiple penetrating arterioles. We hypothesize that the loops and stubs protect blood flow to the parenchyma from an occlusion in a surface vessel. To test this, we assayed the viability of tissue that was sourced by an individual penetrating arteriole following occlusion of a proximal branch in the surface loop. We observed that neurons remained healthy, even when occlusion led to a reduction in the local blood flow. In contrast, direct blockage of a single penetrating arteriole invariably led to neuronal death and formation of a cyst. Our results show that the surface vasculature functions as a grid for the robust allocation of blood in the event of vascular dysfunction. The combined results of the present and prior studies imply that the pial network reallocates blood in response to changing metabolic needs.

Fig. 1.

Complete mapping of the middle cerebral artery. (A) A flattened cortical hemisphere from a fluorescent vascular fill, overlaid with a tracing of all vessels within the middle cerebral artery network. (B) In each tracing, the edges (green lines) connect vertices positioned at branches, with coordination number of 3 (red circles), and vertices positioned at the location of penetrating arteries (cyan circles). (C) Cartoon of the vascular labels that includes penetrating vessels formed en passant and at the end of edges. (D) The composition of vertices between the rats and mice differ slightly, albeit significantly, in the proportion of branches (P < 0.05, t test), but showed no differences in the proportion of vertices at penetrating arterioles. (E) The distribution of edge lengths for the entire pial network. There is a small, but significant shift between the distributions for rats and mice (P < 0.05, KS test, Inset).

Fig. 2.

The backbone loop structure of the pial network. (A) Representative example of a complete MCA tracing for rat. The backbone of the MCA is highlighted with black edges and red vertices, nonbackbone offshoots are shown in green. (B) The ratio of vertices to edges for the combined data from rats and mice is consistent with a scaling of 3 to 2, equal to that for a hexagonal lattice. For comparison, the scaling is 1 for trees and buses. (C) The same backbone as in A, but with the set of all loops, chosen to comprise those with the smallest number of edges involved per loop. The number of edges appears in same color as related vertex. (D) The distribution of number of edges per loop for rats and mice. Despite the difference in the total number of loops, both species share the same distribution.

Fig. 3.

Structural robustness to cumulative edge removal for measured pial networks and ideal lattices. (A) Average backbone robustness to edge removal for networks for rat, mice, and honeycomb lattices of different sizes. Robustness is computed by progressively removing graph edges at random while computing the fractions of vertices that become isolated from the graph's largest component. This process ends with the removal of all edges and it is repeated 10,000 times for each network. The fraction of edges removed that result in isolation of 5% of the vertices are indicated by the color-coded arrows. As a control, the limit in which all vertices approach isolation corresponds to the fraction of vertices that remain disconnected as a path is formed that spans the network. The theoretical value of 2sin(π/18) = 0.347 for percolation in a hexagonal lattice (51) (i.e., the percolation threshold Pc, compares well with the result for simulations with n = 100,000 nodes). (B) The number of vertices required to disconnect 5% of the network as a function of the size of the network. Compared with the rodent MCA backbones, an average of 17 and 40% additional edges have to be removed from a honeycomb or a square lattice, respectively, to attain the same extent of isolated vertices.

Fig. 4.

Penetrating arteries branch from the backbone and directly dive into the parenchyma. (A) Example of offshoot branches emerging from a mouse middle cerebral artery backbone. Offshoot branches were isolated into subgraphs that are color coded by the number of vertices per subgraph. (B) More than 75% of the offshoots consists of a single penetrating arteriole (n = 2,673 and 1,377 offshoot branches for rat and mouse, respectively). The tail of this distribution is empirically bounded by quadratic and cubic decays.

Fig. 5.

Preservation of flux through penetrating arterioles after single-point occlusion of a surface arteriole loop. (A) Maximal projection of a stack of images collected from the upper 300 μm of rat cortical vasculature using in vivo TPLSM. The pial arteriole network is pseudocolored in red and the venous network in blue. The inset highlights a small arteriole loop with three penetrating arteriole stubs. (B) A localized clot is formed in one segment of the surface arteriole loop using targeted photothrombosis (x in loop). Pre- and postocclusion measurements of the flux of RBCs in penetrating arterioles and surface arterioles were collected. Local penetrating arterioles were situated near the targeted surface arteriole, and distant penetrating arterioles were measured as controls. (C) Scatter plot of pre- and postocclusion flux through penetrating arterioles. The histogram of the baseline distribution of flux is derived from 399 arterioles. (D) Photomicrographs of serial sections, stained with αNeuN, from an animal with a surface occlusion that was killed after 1 week of survival. The box indicates the area photographed at higher magnification; arrow in lower set of photomicrographs. The volume of cortical infarction, highlighted by the dashed line, was determined by measuring loss of αNeuN staining across a contiguous set of serial sections. (E) Photomicrographs of serial sections, analyzed as in D, from an animal in which a penetrating arteriole was directly occluded by photothrombosis. Note the relatively large infarction. (F) Microinfarction volumes plotted as a function of the baseline flux of the target arteriole. The experiments shown in D and E are marked with square points.

Fig. 6.

Idealization of the topology and relative scales of the pial vasculature.