General multivariate linear modeling of surface shapes using SurfStat

Abstract

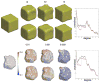
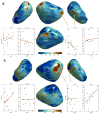
Although there are many imaging studies on traditional ROI-based amygdala volumetry, there are very few studies on modeling amygdala shape variations. This paper presents a unified computational and statistical framework for modeling amygdala shape variations in a clinical population. The weighted spherical harmonic representation is used to parameterize, smooth out, and normalize amygdala surfaces. The representation is subsequently used as an input for multivariate linear models accounting for nuisance covariates such as age and brain size difference using the SurfStat package that completely avoids the complexity of specifying design matrices. The methodology has been applied for quantifying abnormal local amygdala shape variations in 22 high functioning autistic subjects.

Figure 1

Amygdala manual segmentation at (a) axial (b) coronal and (c) midsagittal sections. The amygdala (AMY) was segmented using adjacent structures such as anterior commissure (AC), hippocampus (HIPP), inferior horn of lateral ventricle (IH), optic radiations (OR), optic tract (OT), temporal lobe white matter (TLWM) and tentorial notch (TN).

Figure 2

(a) The heat source (amygdala) is assigned value 1 while the heat sink is assigned the value -1. The diffusion equation is solved with these boundary condition. (b) After a sufficient number of iterations, the equilibrium state f(x,∞) is reached. (c) The gradient field ∇f(x,∞) shows the direction of heat propagation from the source to the sink. The integral curve of the gradient field is computed by connecting one level set to the next level sets of f(x,∞). (d) Amygala surface flattening is done by tracing the integral curve at each mesh vertex. The numbers c = 1.0, 0.6, ⋯ , −1.0 correspond to the level sets f(x,∞) = c. (e) Amygdala surface parameterization using the angles (θ, φ). The point θ = 0 corresponds to the north pole of a unit sphere.

Figure 3

The first (third) row shows the significant Gibbs phenomenon in the spherical harmonic representation of a cube (left amygdala) for degrees k = 18, 42, 78. The second (fourth) row is the weighted spherical harmonic representation at the same degrees but with bandwidth σ = 0.01, 0.001, 0.0001 respectively. The color scale for amygdala is the absolute error between the original and reconstructed amygdale. In almost all degrees, the traditional spherical harmonic representation shows more prominent Gibbs phenomenon compared to the weighted version. The plots display the amount of overshoot for the traditional representation (black) vs. the weighted version (red).

Figure 4

(a) Five representative left amygdala surfaces. (b) 42 degree weighted spherical harmonic representation. Surfaces have different mesh topology. (c) However, meshes can be resampled in such a way that all meshes have identical topology with exactly 2562 vertices and 5120 faces. Identically indexed mesh vertices correspond across different surfaces in the least squares fashion. (d) Spherical harmonic basis Y₂₂ is projected on each amygdala to show surface correspondence. Note that the red colored left most corners more or less align properly.

Figure 5

(a) (b) Simulated surfaces with the known displacement field between them. (c) The displacement in mm. (d) (e) Corresponding weighted spherical harmonic representation (f) The estimated displacement from the weighted spherical harmonic representations.

Figure 6

Simulation results. (a) small bump of height 1.5mm was added to a sphere of radius 10 mm. (b) T-statistic of comparing randomly simulated 20 spheres and 20 bumped spheres showing no group difference (p = 0.35). (c) small bump of height 3mm was added to a sphere of radius 10mm. (d) T-statistic of comparing randomly simulated 20 spheres and 20 bumped spheres showing significant group difference (p < 0.0003).

Figure 7

F statistic map of shape difference displayed on the average left amygdala (a) and right amygdala (b). We did not detect any significant difference at α = 0.01. The left amygdala (a) is displayed in such a way that, if we fold along the dotted lines and connect the identically numbered lines, we obtain the 3D view of the amygdala. The top middle rectangle corresponds to the axial view obtained by observing the amygdala from the top of the brain. (c) and (d) show the F statistic map of shape difference accounting for age and the total brain volume. The arrows in the enlarged area show the direction of shape difference (autism - control).

Figure 8

F statistic map of interaction between group and gaze fixation. Red regions show significant interaction for (a) left and (b) right amygdale. For better visualization, the color bar for the right amygdala (b) has been thresholded at 40 since the maximum F statistics at the largest cluster is 65.68 (p = 0.003). The scatter plots show the particular coordinate of the displacement vector from the average surface vs. gaze fixation. The red lines are regression lines.