MRI quantification of non-Gaussian water diffusion by kurtosis analysis

Abstract

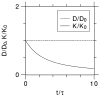
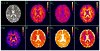
Quantification of non-Gaussianity for water diffusion in brain by means of diffusional kurtosis imaging (DKI) is reviewed. Diffusional non-Gaussianity is a consequence of tissue structure that creates diffusion barriers and compartments. The degree of non-Gaussianity is conveniently quantified by the diffusional kurtosis and derivative metrics, such as the mean, axial, and radial kurtoses. DKI is a diffusion-weighted MRI technique that allows the diffusional kurtosis to be estimated with clinical scanners using standard diffusion-weighted pulse sequences and relatively modest acquisition times. DKI is an extension of the widely used diffusion tensor imaging method, but requires the use of at least 3 b-values and 15 diffusion directions. This review discusses the underlying theory of DKI as well as practical considerations related to data acquisition and post-processing. It is argued that the diffusional kurtosis is sensitive to diffusional heterogeneity and suggested that DKI may be useful for investigating ischemic stroke and neuropathologies, such as Alzheimer's disease and schizophrenia.

Figure 1

Time dependence of the diffusion coefficient and diffusional kurtosis for the Kärger model. The diffusion coefficient is independent of the diffusion time, but the kurtosis decreases on a time scale set by the water exchange time τ.

Figure 2

Comparison of DTI and DKI fitting models. For DTI, the logarithm of diffusion-weighted signal intensity (circles) as a function of the b-value is fit, for small b-values, to a straight line. In brain, this fit is often based on the signal for b = 0 and b = 1000 s/mm². For DKI, the logarithm of the signal intensity is fit, for small b-values, to a parabola. In brain, this fit may be based on the signal for b = 0, b = 1000, and b = 2000 s/mm².

Figure 3

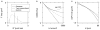
Plots showing the ratio of DKI estimates for (a) the diffusional kurtosis and (b) the diffusion coefficient to the exact values for a two-compartment diffusion model with K = 1. For this model, the water fraction f of the fast diffusing component can vary from 0 to 0.75, as follows from eqn (26). The DKI fits are based on eqns (43) and (44). The dotted lines are references to indicate the ideal estimate ratio of one. Plot (a) shows that the DKI estimate for the kurtosis is accurate to within about 20% if f ≥ 0.52 and Db_max = 2, and plot (b) shows that the DKI estimate for the diffusion coefficient is accurate to within about 7% if Db_max = 2. As indicated by Table 1, f ≈ 0.6 to 0.7 for normal brain, suggesting that DKI with Db_max = 2 should be reasonably accurate. As a comparison, also shown is (c) the ratio of the DTI estimate for the diffusion coefficient to the exact value for the same two-compartment model. The DTI fit is calculated from eqn (35) with b₁ = 0 and b₂ = b_max. The DTI estimate is accurate to within about 20% if Db_max = 1.

Figure 4

Plots showing (a) the water fraction densities for Gaussian, two-compartment, and gamma distribution diffusion models together with the logarithms of the corresponding (b) signal intensities and (c) PDFs. In (a), the vertical lines for the Gaussian and two-compartment models indicate Dirac delta functions with weights proportional to the heights of the lines. For the two-compartment model, the water fraction for the fast diffusing component is f = 2/3. All three models have a diffusion coefficient of D = 1 m μ²/ms, while the Gaussian model has a diffusional kurtosis of K = 0 and the two-compartment and gamma distribution models both have K = 1. Also shown in (b) is the DKI signal intensity of eqn (37) for D = 1 μm²/ms and K = 1, which agrees relatively well with both the two-compartment and gamma distribution models up to b ≈ 2000 s/mm² and with the two-compartment model up to b ≈ 3400 s/mm². The PDFs in (c) assume isotropic diffusion with a diffusion time of t =100 ms, which yields a root-mean-square diffusion length of $\sqrt{6Dt}\approx 24\mu \text{m}$. The PDFs have been normalized by multiplying with a volume element of (100 μm)³. The PDFs for the two-compartment and gamma distribution models both deviate significantly from the Gaussian PDF, as is reflected by their nonzero kurtoses.

Figure 5

DKI diffusion metric maps for a single axial slice together with a T₂-weighted (b = 0) image from one normal subject. The diffusion-weighted data were acquired at 3T with b-values of 0, 1000, and 2000 s/mm². The maps for FA, D̄, D _||, and D_⊥ are similar to those typically obtained with DTI. The maps for K̄, K_||, and K_⊥ provide additional information that quantify diffusional non-Gaussianity. The calibration bars for the diffusivities are in units of μm²/ms, while those for the FA and kurtoses are dimensionless.

Figure 6

Whole brain distribution plots for DKI diffusion metrics for the same subject as in Fig. 4. The distributions were calculated from 45 axial slices each with a thickness of 2.7 mm. Voxels with D̄ > 1.5 μm²/ms were excluded, as they likely contained high amounts of CSF. Each plot was based on 53,881 voxels, corresponding to a total volume of 1060.5 cm³, and a bin size of 0.02 (in units of μm²/ms for the diffusivities). The values in the legends indicate average values ± standard deviations.