Cone beam CT dosimetry: a unified and self-consistent approach including all scan modalities--with or without phantom motion

Abstract

Purpose: This article describes a common methodology and measurement technique, encompassing both conventional (helical and axial) CT scanning using phantom translation and cone beam (or narrow fan beam) CT scans about a stationary phantom. Cone beam CT systems having beam widths along the z-axis wide enough to cover a significant anatomical length (50-160 mm) in a single axial rotation (e.g., in cardiac CT) are rapidly proliferating in the clinic, referred to herein as stationary cone beam CT (SCBCT). The integral format of the CTDI paradigm is not appropriate for a stationary phantom, and is not useful for predicting the dose in SCBCT, nor for perfusion studies or CT fluoroscopy. Likewise, the pencil chamber has limited utility in this domain (even one of extended length).

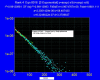
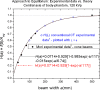
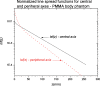
Methods: By demonstrating, both experimentally and theoretically, the match between the dose distribution f(z) for a wide cone beam and that due to an axial scan series D(z), it is shown that the dose on the central ray of the cone beam f(0) is both spatially colocated and numerically equal to the dose predicted by CTDI for the axial series; and thus f(0) is the logical (and unique) choice for a SCBCT dose-descriptor consistent with the CTDI-based dose of conventional CT. This dose f(0) can be readily measured using a conventional (short) ionization chamber. Additionally, Monte Carlo simulations of Boone [J. M. Boone, "Dose spread functions in computed tomography: A Monte Carlo study," Med. Phys. 36, 4547-4554 (2009)], expressed as a scatter LSF (or DSF), allow the application of a convolution-based model [R. L. Dixon, M. T. Munley, and E. Bayram, "An improved analytical model for CT dose simulation with a new look at the theory of CT dose," Med. Phys. 32, 3712-3728 (2005)] of the axial dose profile f(z) for any primary beam width a (any n x T), fan beam and cone beam alike, from a single LSF kernel; its simple form allows the results to be expressed as simple analytical equations. The experimental data of Mori et al. [S. Mori, M. Endo, K. Nishizawa, T. Tsunoo, T. Aoyama, H. Fujiwara, and K. Murase, "Enlarged longitudinal dose profiles in cone-beam CT and the need for modified dosimetry," Med. Phys. 32, 1061-1069 (2005)] from a 256 channel cone beam scanner for a variety of beam widths (28-138 mm) are used to corroborate the theory.

Results: Useful commonalities between SCBCT and conventional CT dose are revealed, including a common equilibrium dose parameter A(eq), which is independent of z-collimator aperture a (or n x T), and a common analytical (exponential growth) function H(lambda) describing the relative approach to scatter equilibrium at z = 0 for both modalities (with lambda = a or lambda = scan length L). This function exhibits good agreement with the above-mentioned cone beam data of Mori et al. for H(a) as well as with data H(L) obtained from conventional CT scanning [R. L. Dixon and A. C. Ballard, "Experimental validation of a versatile system of CT dosimetry using a conventional ion chamber: Beyond CTDI100," Med. Phys. 34(8), 3399-3413 (2007)] for the same directly irradiated, phantom length L = a.

Conclusions: This methodology and associated mathematical theory provide a physically self-consistent description of dose between stationary phantom CT and conventional CT, and has predictive capabilities which can be used to effect a substantial reduction in data collection; provide a bridge between modalities; and predict the relevant peak doses f(0) for perfusion studies.

Figure 1

The axial dose profile f(z) for a wide cone beam of widtha=138 mm generated by a single rotation about a stationary phantom (○) exhibits little difference from the accumulated dose distribution ${\tilde{D}}_N\left(z\right)$ (●) due to the superposition of N=5 axial profiles $\widehat{f}\left(z\right)$ having $\widehat{a}=28\text{\hspace{0.5em}mm}$ spaced at intervals (a table increment of) $b=\widehat{a}=28\text{\hspace{0.5em}mm}$, with a resulting a scan length $L=N\widehat{a}=140\text{\hspace{0.5em}mm}$; giving essentially the same directly irradiated length (L=a) as the cone beam having a=138 mm. The peak doses atz=0 are essentially equal, ${\tilde{D}}_N\left(0\right)\approx f\left(0\right)=1.0$, thereby corroborating the choice of f(0) to represent the dose for SCBCT.

Figure 2

Scatter LSF, central axis 32 cm diameter PMMA body phantom with double-exponential fit function (arbitrary units). Data from a Monte Carlo simulation (Ref. 17) at 120 kVp with a body bow-tie filter.

Figure 3

Approach to scatter equilibrium theory vs experiment. Relative approach to equilibrium function H(a)=f(0)∕f_eq(0)=f(0)∕A_eq on the central axis of a stationary phantom (e.g., SCBCT). The solid circles (●) are the experimental data of Mori presented in Table 1. The solid and dashed lines representing H(a) are not empirical fits but rather theoretical predictions obtained from the mathematical model; the solid black line representing the full double-exponential scatter lsf Eq. 16, and the essentially congruent dotted-dashed line using the simpler single-exponential approximation of the scatter lsf Eq. 17. Also plotted is the experimental approach to equilibrium data for conventional CT scans measured on GE 16 channel and 64 channel scanners for scan lengths L from 100 to 400 mm, and plotted (○) using the correspondence L=a; thus validating the same functional form for both modalities, H(L)=H(a) with the correspondence a=L.

Figure 4

Scatter lsf for the central and peripheral axes in a 32 cm diameter PMMA phantom normalized to unit area. The actual LSF=η×lsf, where η=S∕P ratio with η=13 for the central axis and η=1.5 for the peripheral axis (Ref. 17); thus the absolute peripheral axis LSF falls below that for the central axis as expected.

Figure 5

Approach to equilibrium function H(a^′) on the peripheral (edge) axis of the body phantom plotted vs the FWHM a^′ of the cone beam dose profile f(z) on that axis, together with the experimental data of Mori (Ref. 1) and helical scan data (Ref. 2) plotted using L=a^′.