Experimental validation of convection-diffusion discretisation scheme employed for computational modelling of biological mass transport
- PMID: 20642816
- PMCID: PMC2918622
- DOI: 10.1186/1475-925X-9-34
Experimental validation of convection-diffusion discretisation scheme employed for computational modelling of biological mass transport
Abstract
Background: The finite volume solver Fluent (Lebanon, NH, USA) is a computational fluid dynamics software employed to analyse biological mass-transport in the vasculature. A principal consideration for computational modelling of blood-side mass-transport is convection-diffusion discretisation scheme selection. Due to numerous discretisation schemes available when developing a mass-transport numerical model, the results obtained should either be validated against benchmark theoretical solutions or experimentally obtained results.
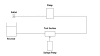
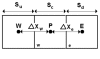
Methods: An idealised aneurysm model was selected for the experimental and computational mass-transport analysis of species concentration due to its well-defined recirculation region within the aneurysmal sac, allowing species concentration to vary slowly with time. The experimental results were obtained from fluid samples extracted from a glass aneurysm model, using the direct spectrophometric concentration measurement technique. The computational analysis was conducted using the four convection-diffusion discretisation schemes available to the Fluent user, including the First-Order Upwind, the Power Law, the Second-Order Upwind and the Quadratic Upstream Interpolation for Convective Kinetics (QUICK) schemes. The fluid has a diffusivity of 3.125 x 10-10 m2/s in water, resulting in a Peclet number of 2,560,000, indicating strongly convection-dominated flow.
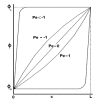
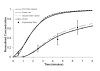
Results: The discretisation scheme applied to the solution of the convection-diffusion equation, for blood-side mass-transport within the vasculature, has a significant influence on the resultant species concentration field. The First-Order Upwind and the Power Law schemes produce similar results. The Second-Order Upwind and QUICK schemes also correlate well but differ considerably from the concentration contour plots of the First-Order Upwind and Power Law schemes. The computational results were then compared to the experimental findings. An average error of 140% and 116% was demonstrated between the experimental results and those obtained from the First-Order Upwind and Power Law schemes, respectively. However, both the Second-Order upwind and QUICK schemes accurately predict species concentration under high Peclet number, convection-dominated flow conditions.
Conclusion: Convection-diffusion discretisation scheme selection has a strong influence on resultant species concentration fields, as determined by CFD. Furthermore, either the Second-Order or QUICK discretisation schemes should be implemented when numerically modelling convection-dominated mass-transport conditions. Finally, care should be taken not to utilize computationally inexpensive discretisation schemes at the cost of accuracy in resultant species concentration.
Figures
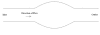


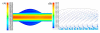
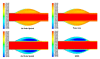
Similar articles
-
Finite volume schemes for the numerical simulation of tracer transport in plants.Math Biosci. 2017 Jun;288:14-20. doi: 10.1016/j.mbs.2017.02.009. Epub 2017 Feb 17. Math Biosci. 2017. PMID: 28216295
-
Dispersion modeling in pore networks: A comparison of common pore-scale models and alternative approaches.J Contam Hydrol. 2020 Jan;228:103578. doi: 10.1016/j.jconhyd.2019.103578. Epub 2019 Nov 13. J Contam Hydrol. 2020. PMID: 31767229
-
Finite Element Implementation of Computational Fluid Dynamics With Reactive Neutral and Charged Solute Transport in FEBio.J Biomech Eng. 2023 Sep 1;145(9):091011. doi: 10.1115/1.4062594. J Biomech Eng. 2023. PMID: 37219843 Free PMC article.
-
Stochastic Hydrodynamics of Complex Fluids: Discretisation and Entropy Production.Entropy (Basel). 2022 Feb 9;24(2):254. doi: 10.3390/e24020254. Entropy (Basel). 2022. PMID: 35205548 Free PMC article. Review.
-
Oxygen supply to contracting skeletal muscle at the microcirculatory level: diffusion vs. convection.Acta Physiol Scand. 2000 Apr;168(4):593-602. doi: 10.1046/j.1365-201x.2000.00710.x. Acta Physiol Scand. 2000. PMID: 10759595 Review.
Cited by
-
Impact of Tissue Factor Localization on Blood Clot Structure and Resistance under Venous Shear.Biophys J. 2018 Feb 27;114(4):978-991. doi: 10.1016/j.bpj.2017.12.034. Biophys J. 2018. PMID: 29490257 Free PMC article.
-
Computational Study of Thrombus Formation and Clotting Factor Effects under Venous Flow Conditions.Biophys J. 2016 Apr 26;110(8):1869-1885. doi: 10.1016/j.bpj.2016.03.010. Biophys J. 2016. PMID: 27119646 Free PMC article.
References
-
- Walsh MT, Kavanagh EG, O'Brien T, Grace PA, McGloughlin T. On the existence of an optimum end-to-side junctional geometry in peripheral bypass surgery - a computer generated study. European Journal of Vascular and Endovascular Surgery. 2003;26:649–656. doi: 10.1016/j.ejvs.2003.08.004. - DOI - PubMed
-
- Morris L, Delassus P, Walsh M, McGloughlin T. A mathematical model to predict the in vivo pulsatile drag forces acting on bifurcated stent grafts used in Endovascular treatment of abdominal aortic aneurysms (AAA) Journal of Biomechanics. 2004;37:1087–1095. doi: 10.1016/j.jbiomech.2003.11.014. - DOI - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Miscellaneous

