Mathematical modeling of K-Ras nanocluster formation on the plasma membrane
- PMID: 20643072
- PMCID: PMC2905126
- DOI: 10.1016/j.bpj.2010.04.055
Mathematical modeling of K-Ras nanocluster formation on the plasma membrane
Abstract
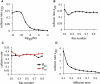
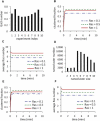
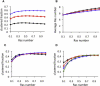
K-Ras functions as a critical node in the mitogen-activated protein kinase (MAPK) pathway that regulates key cellular functions including proliferation, differentiation, and apoptosis. Following growth factor receptor activation K-Ras.GTP forms nanoclusters on the plasma membrane through interaction with the scaffold protein galectin-3. The generation of nanoclusters is essential for high fidelity signal transduction via the MAPK pathway. To explore the mechanisms underlying K-Ras.GTP nanocluster formation, we developed a mathematical model of K-Ras-galectin-3 interactions. We designed a computational method to calculate protein collision rates based on experimentally determined protein diffusion rates and diffusion mechanisms and used a genetic algorithm to search the values of key model parameters. The optimal estimated model parameters were validated using experimental data. The resulting model accurately replicates critical features of K-Ras nanoclustering, including a fixed ratio of clustered K-Ras.GTP to monomeric K-Ras.GTP that is independent of the concentration of K-Ras.GTP. The model reproduces experimental results showing that the cytosolic level of galectin-3 determines the magnitude of the K-Ras.GTP clustered fraction and illustrates that nanoclustering is regulated by key nonequilibrium processes. Our kinetic model identifies a potential biophysical mechanism for K-Ras nanoclustering and suggests general principles that may be relevant for other plasma-membrane-localized proteins.
Copyright (c) 2010 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures


Similar articles
-
Ras and the Plasma Membrane: A Complicated Relationship.Cold Spring Harb Perspect Med. 2018 Oct 1;8(10):a031831. doi: 10.1101/cshperspect.a031831. Cold Spring Harb Perspect Med. 2018. PMID: 29229665 Free PMC article. Review.
-
K-ras nanoclustering is subverted by overexpression of the scaffold protein galectin-3.Cancer Res. 2008 Aug 15;68(16):6608-16. doi: 10.1158/0008-5472.CAN-08-1117. Cancer Res. 2008. PMID: 18701484 Free PMC article.
-
Electrostatic interactions positively regulate K-Ras nanocluster formation and function.Mol Cell Biol. 2008 Jul;28(13):4377-85. doi: 10.1128/MCB.00050-08. Epub 2008 May 5. Mol Cell Biol. 2008. PMID: 18458061 Free PMC article.
-
Nucleophosmin and nucleolin regulate K-Ras plasma membrane interactions and MAPK signal transduction.J Biol Chem. 2009 Oct 9;284(41):28410-28419. doi: 10.1074/jbc.M109.001537. Epub 2009 Aug 6. J Biol Chem. 2009. PMID: 19661056 Free PMC article.
-
GTP hydrolysis mechanism of Ras-like GTPases.J Mol Biol. 2004 Jul 23;340(5):921-32. doi: 10.1016/j.jmb.2004.06.007. J Mol Biol. 2004. PMID: 15236956 Review.
Cited by
-
The Nanoscale Organization of the Plasma Membrane and Its Importance in Signaling: A Proteolipid Perspective.Plant Physiol. 2020 Apr;182(4):1682-1696. doi: 10.1104/pp.19.01349. Epub 2019 Dec 19. Plant Physiol. 2020. PMID: 31857424 Free PMC article. Review.
-
Lifetime of actin-dependent protein nanoclusters.Biophys J. 2023 Jan 17;122(2):290-300. doi: 10.1016/j.bpj.2022.12.015. Epub 2022 Dec 14. Biophys J. 2023. PMID: 36518075 Free PMC article.
-
Signal integration by lipid-mediated spatial cross talk between Ras nanoclusters.Mol Cell Biol. 2014 Mar;34(5):862-76. doi: 10.1128/MCB.01227-13. Epub 2013 Dec 23. Mol Cell Biol. 2014. PMID: 24366544 Free PMC article.
-
Ras and the Plasma Membrane: A Complicated Relationship.Cold Spring Harb Perspect Med. 2018 Oct 1;8(10):a031831. doi: 10.1101/cshperspect.a031831. Cold Spring Harb Perspect Med. 2018. PMID: 29229665 Free PMC article. Review.
-
Ras trafficking, localization and compartmentalized signalling.Semin Cell Dev Biol. 2012 Apr;23(2):145-53. doi: 10.1016/j.semcdb.2011.09.002. Epub 2011 Sep 8. Semin Cell Dev Biol. 2012. PMID: 21924373 Free PMC article. Review.
References
-
- Cox A.D., Der C.J. The dark side of Ras: regulation of apoptosis. Oncogene. 2003;22:8999–9006. - PubMed
-
- Downward J. Targeting RAS signalling pathways in cancer therapy. Nat. Rev. Cancer. 2003;3:11–22. - PubMed
-
- Bhalla U.S., Ram P.T., Iyengar R. MAP kinase phosphatase as a locus of flexibility in a mitogen-activated protein kinase signaling network. Science. 2002;297:1018–1023. - PubMed
-
- Tian T., Harding A., Hancock J.F. Plasma membrane nanoswitches generate high-fidelity Ras signal transduction. Nat. Cell Biol. 2007;9:905–914. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

